
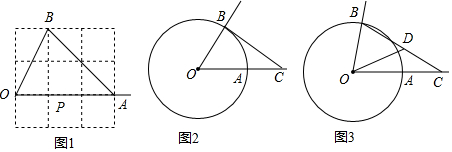
分析 (1)根据射影值的定义一一判断即可解决问题.
(2)①根据两边成比例夹角相等的两个三角形相似,可得△BOH∽△COB,推出∠BHO=∠CBO=90°,由此即可证明;
②图形是上下对称的,只考虑B在直线OC上以及OC上方部分的情形.分两种情形考虑:当∠DOB<90°时,当∠DOB≥90°时.
解答 解:(1)①错误.点B在射线OA上的射影值小于1时,∠OBA可以是钝角,故△OAB不一定是锐角三角形.
②正确.点B在射线OA上的射影值等于1时,AB⊥OA,∠OAB=90°,△ABC是直角三角形.
③正确.B在射线OA上的射影值大于1时,∠OAB是钝角,△ABC是钝角三角形.故答案为B.
(2)①如图2中,作BH⊥OC于H.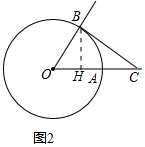
∵$\frac{OH}{OC}$=$\frac{1}{2}$,$\frac{OB}{OC}$=$\frac{1}{2}$,OA=OB=OC=1,
∴$\frac{OH}{OB}$=$\frac{OB}{OC}$,∵∠BOH=∠COB,
∴△BOH∽△COB,
∴∠BHO=∠CBO=90°,
∴BC⊥OB,
∴BC是⊙O的切线.
②图形是上下对称的,只考虑B在直线OC上以及OC上方部分的情形.
当∠DOB<90°时,设DM=h,
∵BD=DC,
∴S△OBD=S△ODC,
∴$\frac{1}{2}$•OB•DN=$\frac{1}{2}$•OC•DM,
∴DN=2h
∵OD2=DN2+ON2=DM2+OM2,
∴4h2+y2=h2+x2,
∴3h2=x2-y2 ①,
∵BD2=CD2,
∴4h2+(1-y)2=h2+(2-x)2 ②,
①②消去y得到y=2x-$\frac{3}{2}$.
如图,当∠BOD=90°时,
在Rt△ODM中,易知OD=2DM,
∴∠DOM=30°,设DM=h,则OD=2h.OM=$\sqrt{3}$h,
∴h2+(2-$\sqrt{3}$h)2=12+4h2,
∴h=$\frac{\sqrt{3}}{4}$,
∴OM=$\frac{3}{4}$,
当点B在OC上时,OD=$\frac{1}{2}$,
综上所述,当$\frac{1}{2}$≤x≤$\frac{3}{4}$时,y=0,
当$\frac{3}{4}$<x$≤\frac{3}{2}$时,y=2x-$\frac{3}{2}$.
点评 本题考查圆综合题、相似三角形的判定和性质、勾股定理、射影值的定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{2}{3}$ | B. | m<$\frac{1}{2}$ | C. | m=$\frac{2}{3}$ | D. | m=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
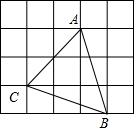 如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )
如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )| A. | $\frac{3}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
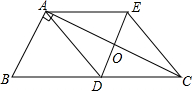 如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.
如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段 | 频数 | 频率 |
| 72分以下 | 368 | 0.2 |
| 72----80分 | 460 | 0.25 |
| 81----95分 | 644 | 0.35 |
| 96----108分 | 184 | 0.2 |
| 109----119分 | 130 | |
| 120分 | 54 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②都是 | B. | ①②都不是 | C. | ①是②不是 | D. | ①不是②是 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com