
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG= ![]() BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE= ![]() S矩形ABCD
S矩形ABCD
A.1
B.2
C.3
D.4
【答案】C
【解析】解:∵EF⊥AC,点G是AE中点, ∴OG=AG=GE= ![]() AE, ∵∠AOG=30°, ∴∠OAG=∠AOG=30°, ∠GOE=90°-∠AOG=90°-30°=60°, ∴△OGE是等边三角形,故(3)正确; 设AE=2a,则OE=OG=a, 由勾股定理得,AO=
AE, ∵∠AOG=30°, ∴∠OAG=∠AOG=30°, ∠GOE=90°-∠AOG=90°-30°=60°, ∴△OGE是等边三角形,故(3)正确; 设AE=2a,则OE=OG=a, 由勾股定理得,AO= ![]() =
= ![]() =
= ![]() a, ∵O为AC中点, ∴AC=2AO=2
a, ∵O为AC中点, ∴AC=2AO=2 ![]() a, ∴BC=
a, ∴BC= ![]() AC=
AC= ![]() ×2
×2 ![]() a=
a= ![]() a, 在Rt△ABC中,由勾股定理得,AB=
a, 在Rt△ABC中,由勾股定理得,AB= ![]() =3a, ∵四边形ABCD是矩形, ∴CD=AB=3a, ∴DC=3OG,故(1)正确; ∵OG=a,
=3a, ∵四边形ABCD是矩形, ∴CD=AB=3a, ∴DC=3OG,故(1)正确; ∵OG=a, ![]() BC=
BC= ![]() a, ∴OG≠
a, ∴OG≠ ![]() BC,故(2)错误; ∵S△AOE=
BC,故(2)错误; ∵S△AOE= ![]() ·
· ![]() a·2a=
a·2a= ![]() S矩形ABCD=3a
S矩形ABCD=3a ![]() =3
=3 ![]() a2∴S△AOE=
a2∴S△AOE= ![]() S矩形ABCD , 故(4)正确; 综上所述,结论正确是(1)(3)(4)共3个. 故选:C.
S矩形ABCD , 故(4)正确; 综上所述,结论正确是(1)(3)(4)共3个. 故选:C.
【考点精析】根据题目的已知条件,利用等边三角形的判定和勾股定理的概念的相关知识可以得到问题的答案,需要掌握三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
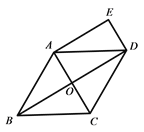
求证:四边形AODE是矩形;(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题: 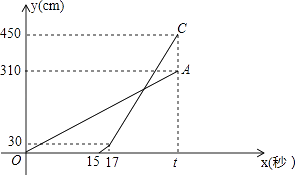
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm,t=;
(2)当x为何值时,乙追上了甲?
(3)若两台机器人到达终点Q后迅速折返,并保持折返前的速度继续匀速行走返回到点P,乙比甲早到多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)15+(-![]() )-15-(-0.25) (2) (-81)÷
)-15-(-0.25) (2) (-81)÷![]() ×
×![]() ÷(-32)
÷(-32)
(3)29![]() ×(-12) (4)25×
×(-12) (4)25×![]() -(-25)×
-(-25)×![]() +25×(-
+25×(-![]() )
)
(5)-24-(-4)2 ×(-1)+(-3)3 (6)3.25-[(-![]() )-(-
)-(-![]() )+(-
)+(-![]() )+
)+![]() ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校. 图中的折线表示清清的行程s(米)与所花时间t (分)之间的函数关系. 下列说法错误的是( )

A. 清清等公交车时间为3分钟 B. 清清步行的速度是80米/分
C. 公交车的速度是500米/分 D. 清清全程的平均速度为290米/分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示.请根据图象回答下列问题:
(1)小敏去超市途中的速度是多少?在超市逗留了多少时间?
(2)小敏几点几分返回到家?
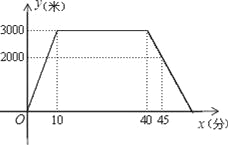
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.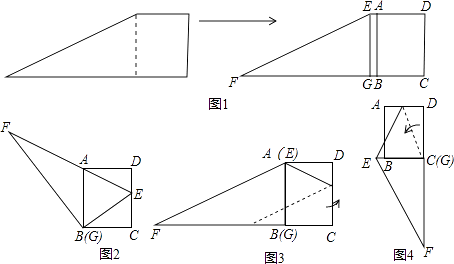
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度;
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com