
【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?
科目:初中数学 来源: 题型:
【题目】某种动物的身高y(dm)是其腿长x(dm)的一次函数.当动物的腿长为6dm时,身高为45.5dm;当动物的腿长为14dm时,身高为105.5dm.
(1)写出y与x之间的关系式;
(2)当该动物腿长10dm时,其身高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习几何的一个重要方法就是要学会抓住基本图形,让我们来做一次研究性学习.

(1)如图①所示的图形,像我们常见的学习用品一圆规,我们常把这样的图形叫做“规形图”.请你观察“规形图”,试探究∠BOC与∠A、∠B、∠C之间的关系,并说明理由:
(2)如图②,若△ABC中,BO平分∠ABC,CO平分∠ACB,且它们相交于点O,试探究∠BOC与∠A的关系;
(3)如图③,若△ABC中,∠ABO=![]() ∠ABC,∠ACO=
∠ABC,∠ACO=![]() ∠ACB,且BO、CO相交于点O,请直接写出∠BOC与∠A的关系式为 _.
∠ACB,且BO、CO相交于点O,请直接写出∠BOC与∠A的关系式为 _.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.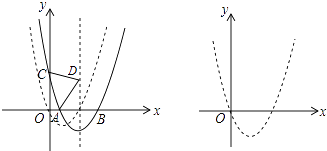
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定:T(x,y)=![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(2,1)=![]()
①求a,b的值;
②若关于m的不等式组![]() 恰好有3个整数解,求p的取值范围;
恰好有3个整数解,求p的取值范围;
(2)若T(x,y)=T(y,x)对任意有理数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直线y=﹣x沿y轴向下平移后的直线恰好经过点A(2,﹣4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中点A、B在坐标轴上,其中A(0,a),B(b,0),满足|a﹣3|+![]() =0.
=0.

(1)求点A、B的坐标;
(2)将AB平移到CD,点A对应点C(﹣2,m),若△ABC面积为13,连接CO,求点C的坐标;
(3)在(2)的条件下,求证:∠AOC=∠OAB+∠OCD;
(4)如图2,若AB∥CD,点C、D也在坐标轴上,点F为线段AB上一动点(不包含A、B两点),连接OF,FP平分∠BFO,∠BCP=2∠PCD,试证明:∠COF=3∠P﹣∠OFP(提示:可直接利用(3)的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在疫情期间利用网络组织了一次防“新冠病毒”知识竞赛,评出特等奖10人,优秀奖20人.学校决定给所有获奖学生各发一份奖品,同一等次的奖品相同.
(1)(列方程组解应用题)若特等奖和优秀奖的奖品分别是口罩和温度计,口罩单价的2倍与温度计单价的3倍相等,购买这两种奖品一共花费700元,求口罩和温度计的单价各是多少元?
(2)(利用不等式或不等式组解应用题)若两种奖品的单价都是整数,且要求特等奖单价比优秀奖单价多20元.在总费用不少于440而少于500元的前提下,购买这两种奖品时它们的单价有几种情况,请分别求出每种情况特等奖和优秀奖奖品的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究“掷一枚图钉,钉尖朝上”的概率,两个小组用同一个图钉做试验进行比较,他们的统计数据如下:
掷图钉的次数 | 50 | 100 | 200 | 300 | 400 |
钉尖朝上 的次数 | |||||
第一小组 | 23 | 39 | 79 | 121 | 160 |
第二小组 | 24 | 41 | 81 | 124 | 164 |
(1)请你估计第一小组和第二小组所得的概率分别是多少?
(2)你认为哪一个小组的结果更准确?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com