
【题目】如图,在每个小正方形的边长为1的网格中,点![]() ,
,![]() ,
,![]() ,
,![]() 均在格点上,点
均在格点上,点![]() 是在直线
是在直线![]() 上的动点,连
上的动点,连![]() ,点
,点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点.
的对称点.
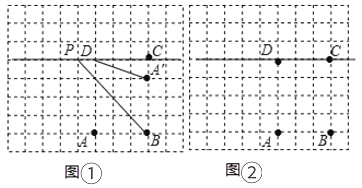
(1)在图①中,当![]() (点
(点![]() 在点
在点![]() 的左侧)时,计算
的左侧)时,计算![]() 的值等于______.
的值等于______.
(2)当![]() 取得最小值时,请在如图②所示的网格中,用无刻度的直尺画出点
取得最小值时,请在如图②所示的网格中,用无刻度的直尺画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的.(不要求证明)
的位置是如何找到的.(不要求证明)
科目:初中数学 来源: 题型:
【题目】某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,从这10个部门中随机抽取了![]() 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.![]() .
.![]() 部门每日餐余重量的频数分布直方图如下(数据分成6组:
部门每日餐余重量的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):
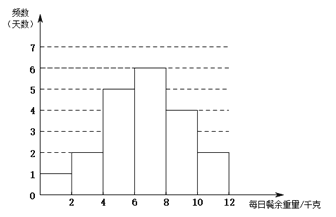
![]() .
.![]() 部门每日餐余重量在
部门每日餐余重量在![]() 这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() 部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() 两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
部门 | 平均数 | 中位数 | 众数 |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
根据以上信息,回答下列问题:
(1)写出表![]() 中的值;
中的值;
(2)在![]() 这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“
这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“![]() ”或“
”或“![]() ”),理由是____________;
”),理由是____________;
(3)结合![]() 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 在
在![]() 轴负半轴上,且
轴负半轴上,且![]() .
.
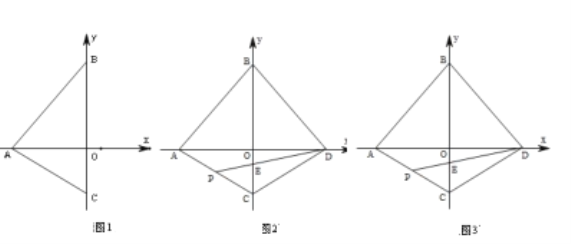
(1)求![]() 的值;
的值;
(2)把![]() 沿
沿![]() 轴翻折,使点
轴翻折,使点![]() 落在
落在![]() 轴的点
轴的点![]() 处,点
处,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 横坐标为
横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 、
、![]() 的函数解析式(用含
的函数解析式(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)在(2)的条件下,若![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
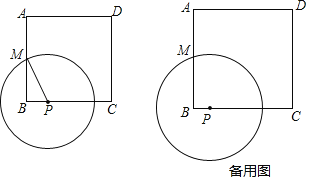
【题目】如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.
(1)当BP= 时,△MBP~△DCP;
(2)当⊙P与正方形ABCD的边相切时,求BP的长;
(3)设⊙P的半径为x,请直接写出正方形ABCD中恰好有两个顶点在圆内的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
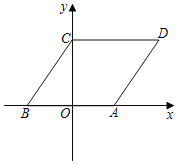
【题目】如图,在平面直角坐标系中,菱形ABCD的边AB在x轴上,点B坐标(﹣3,0),点C坐标(0,4),点P从原点O出发,以每秒一个单位长度的速度沿x轴正方向移动,移动时间为t(0≤t≤5)秒,过点P作平行于y轴的直线l,直线l扫过四边形OCDA的面积为S.
(1)求直线AD的函数表达式;
(2)当S=![]() 时,请直接写出t的值;
时,请直接写出t的值;
(3)如果点M是(2)中的直线1上的点,点N在x轴上,并且以A,D,M,N为顶点的四边形是平行四边形,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
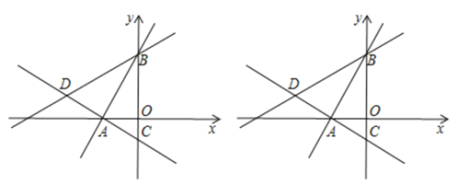
【题目】如图所示,在平面直角坐标系中,过点![]() 的两条直线分别交
的两条直线分别交![]() 轴于
轴于![]() ,
,![]() 两点,且
两点,且![]() 、
、![]() 两点的纵坐标分别是一元二次方程
两点的纵坐标分别是一元二次方程![]() 的两个根.
的两个根.
(1)试问:直线![]() 与直线
与直线![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在直线![]() 上寻找点
上寻找点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰三角形,请直接写出
三点为顶点的三角形是等腰三角形,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
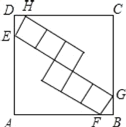
【题目】如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
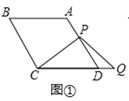
【题目】在菱形![]() 中,
中,![]() 为直线
为直线![]() 上的点,
上的点,![]() 为直线
为直线![]() 上的点,分别连接
上的点,分别连接![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,点
,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,如图①,易证:
的延长线上,如图①,易证:![]() (不需证明);
(不需证明);
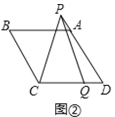
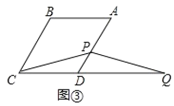
(2)如图②,若∠B=120°,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,如图③,猜想线段
的延长线上,如图③,猜想线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com