
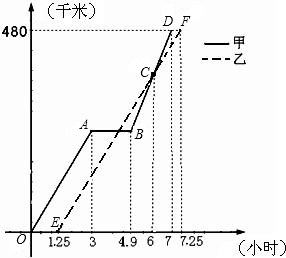
 示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
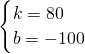 ∴直线EF的解析式是y乙=80x-100;
∴直线EF的解析式是y乙=80x-100; ;
;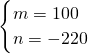 ;∴BD的解析式是y甲=100x-220;
;∴BD的解析式是y甲=100x-220;

科目:初中数学 来源: 题型:
 示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 自从2008年5月12日我国四川地区发生特大地震以来,全国人民“众志成城 抗震救灾”,纷纷捐款献爱心,在某校的一次捐款活动中,九年级(1)班30名学生捐款情况如下表:
自从2008年5月12日我国四川地区发生特大地震以来,全国人民“众志成城 抗震救灾”,纷纷捐款献爱心,在某校的一次捐款活动中,九年级(1)班30名学生捐款情况如下表:| 捐款(单位:元) | 20 | 50 | 100 | 150 | 200 |
| 人数 | 4 | 12 | 9 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com