
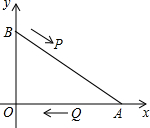
 如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题:
如图,在直角坐标系中,已知点A(8,0)、B(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<$\frac{10}{3}$)秒.解答如下问题:分析 (1)分两种情形讨论①当$\frac{PA}{AB}$=$\frac{AQ}{OA}$时,△APQ∽△ABO,②当$\frac{AP}{OA}$=$\frac{AQ}{AB}$时,△APQ∽△AOB,分别列出方程计算即可.
(2)过点P作过点P作PD⊥x轴于点D,构造平行线PD∥BO,由线段比例关系 $\frac{AP}{AB}$=$\frac{PD}{OB}$ 求得PD,依据三角形的面积公式可求得S与t之间的函数关系式是一个关于t的二次函数,利用二次函数求极值的方法求出S的最大值.
解答 解:(1)如图①中,
在Rt△ABO中,由勾股定理得:AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=10.
①当$\frac{PA}{AB}$=$\frac{AQ}{OA}$时,△APQ∽△ABO,
即$\frac{10-3t}{10}$=$\frac{2t}{8}$,t=$\frac{20}{11}$.
②当$\frac{AP}{OA}$=$\frac{AQ}{AB}$时,△APQ∽△AOB,
即$\frac{10-3t}{8}$=$\frac{2t}{10}$,t=$\frac{50}{23}$,
综上所述,t=$\frac{20}{11}$s或$\frac{50}{23}$s时,△PAQ与△AOB相似.
(2)如图②所示:过点P作PD⊥x轴于点D.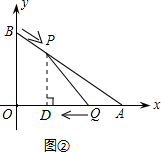
∵PD⊥x轴,OB⊥x轴,
∴OB∥PD.
∴$\frac{AP}{AB}$=$\frac{PD}{OB}$,即 $\frac{10-3t}{10}$=$\frac{PD}{6}$.
∴PD=6-$\frac{9}{5}$t.
由三角形的面积公式可知:S=$\frac{1}{2}$AQ•PD=$\frac{1}{2}$•2t•(6-$\frac{9}{5}$t)=6t-$\frac{9}{5}$t2.
∴S与t的函数关系式为y=-$\frac{9}{5}$t2+6t.
∴S=-$\frac{9}{5}$(t-$\frac{5}{3}$)2+5.
∴当t=$\frac{5}{3}$s时,S有最大值,最大值为5(平方单位).
点评 本题主要考查的是动点问题的函数图象、配方法求二次函数的最值、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,灵活运用所学知识解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 长方形的长一定时,其面积y与宽x | |
| B. | 高速公路上匀速行驶的汽车,其行驶的路程y与行驶的时间x | |
| C. | y=|x| | |
| D. | |y|=x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
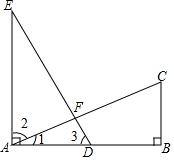 如图,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,则下面式子中不能成立的是( )
如图,已知EA⊥AB,BC∥EA,EA=AB=2BC,D为AB的中点,则下面式子中不能成立的是( )| A. | ∠1+∠3=90° | B. | DE⊥AC且DE=AC | C. | ∠3=60° | D. | ∠2=∠3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com