
解答题
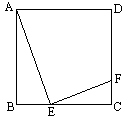
正方形ABCD的边长为4cm,E在BC上,F在DC上,AE⊥EF,如图,BE=x cm,CF=y cm,求y与x的函数关系式.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:新课标3维同步训练与评价·数学·九年级·上 题型:044
解答题
(1)已知:如图△ABC为正三角形,点M为BC边上任意一点,点N为CA边上任意一点,且BM=CA,BN与AM相交于Q点,试求∠BQM的度数.
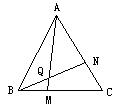
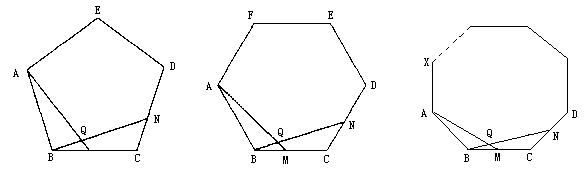
(2)如果将(1)中的正三角形改为正方形ABCD,(如下图)点M为BC边上任意一点,点N为CD边上任意一点,且BM=CN,BN与AM相交于Q点,那么∠BQM等于多少度呢?说明理由.

(3)如果将(1)中的“正三角形”改为正五边形……正n边形,其它条件都不变,请你根据(1)(2)的求解思路,将你推断的结论填入下表.

查看答案和解析>>
科目:初中数学 来源:同步练习 数学九年级下册 题型:044
解答题
如图,锐角三角形ABC的边BC的长为6,面积为12,P在AB上,Q在AC上,且PQ∥BC,正方形PQRS的边长为x,正方形PQRS与△ABC的公共部分的面积为y.
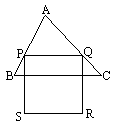
(1)当SR恰落在BC上时,求x;
(2)当SR落在△ABC外部时,求y与x之间的函数关系式,并求x的取值范围;
(3)当x为何值时,y取最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读下面的问题,并解答题(1)和题(2)。
如图①所示,P是等腰△ABC的底边BC上任一点,PE⊥AB于E,PF⊥AC于F,BH是腰AC上的高,求证:PE+PF=BH。

![]() ,
,
![]()
因为AB=AC,所以BH=PE+PF
按照上述证法或用其它方法证明下面两题:
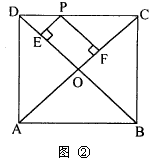
(1)如图②,P是边长为2的正方形ABCD边CD上任意一点,且PE⊥DB于E,PF⊥CA于F,求PE+PF的值。
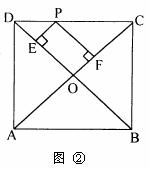
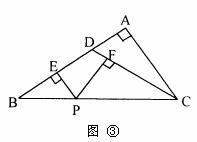
(2)如图③,在△ABC中,∠A=90°,D是AB上一点,且BD=CD,过BC
![]()
求PE+PF的值
查看答案和解析>>
科目:初中数学 来源:期末题 题型:探究题
| 阅读下面的问题,并解答题(1)和题(2)。 | ||
(1)如图②,P是边长为2的正方形ABCD边CD上任意一点,且PE⊥DB于E,PF⊥CA于F,求PE+PF的值。 | ||
 | ||
(2)如图③,在△ABC中,∠A=90°,D是AB上一点,且BD=CD,过BC上任一点P做PE⊥AB于E,PF⊥DC于F,已知AD:BD=1:3,BC= 4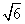 ,求PE+PF的值。 ,求PE+PF的值。 | ||
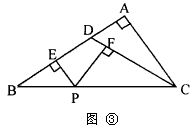 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com