
【题目】如图,△ABC 中,点 E,F,G 分别在 BC,AC,AB 上,AE 与 BF 交于点 O,且点 O 在 CG 上,根据尺规作图的痕迹,判断下列说法不正确的是( )

A.AE,BF 是△ABC 的角平分线B.点 O 到△ABC 三边的距离相等
C.CG 也是△ABC 的一条角平分线D.AO=BO=CO
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
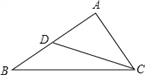
【题目】如图,已知在△ABC中,D是AB的中点,且∠ACD=∠B,若 AB=10,求AC的长.
【答案】5![]() .
.
【解析】试题分析:
由点D是AB的中点,AB=10,易得AD=5;再由∠ACD=∠B,∠A=∠A,可证得:
△ACD∽△ABC,从而可得: ![]() ,由此得到:AC2=AD
,由此得到:AC2=AD![]() AB=50即可解得AC的值.
AB=50即可解得AC的值.
试题解析:
∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC.
∴![]() ,
,
∴AC2=AD![]() AB.
AB.
∵D是AB的中点,AB=10,
∴AD=![]() AB=5,
AB=5,
∴AC2=50.
解得AC=![]() .
.
【题型】解答题
【结束】
22
【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.

(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB 中,∠AOB=90°,OA=3,OB=4,将△AOB 沿 x 轴依次以三角形三个顶点为旋转中心顺时针旋转,分别得图②,图③,…,则旋转到图⑩时直角顶点的坐标是( )

A.(28,4)B.(36,0)C.(39,0)D.(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3
与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3
(1)求抛物线所对应的函数解析式;
(2)求ΔABC的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△AOB中,∠AOB=90°,以顶点O为原点,分别以OA、OB所在直线为x轴、y轴建立平面直角坐标系(如图),点A(a,0),B(0,b)满足![]() +|a-2|=0
+|a-2|=0

(1)点A的坐标为 ;点B的坐标为 .
(2)如图①,已知坐标轴上有两动点D、E同时出发,点D从A点出发沿x轴负方向以每秒1个单位长度的速度匀速移动,点E从O点出发以每秒2个单位长度的速度沿y轴正方向移动,点E到达B点时运动结束,AB的中点C的坐标是(1,2),设运动时间为t(t>0)秒,问:是否存在这样的t,使S△OCD=S△OCE?若存在,请求出t的值:若不存在,请说明理由.
(3)如图②,点F是线段AB上一点,满足∠FOA=∠FAO,点G是第二象限中一点,连OG使得∠BOG=∠BOF,点P是线段OB上一动点,连AP交OF于点Q,当点P在线段OB上运动的过程中,![]() 的值是否会发生变化?若不变,请求出k的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出k的值;若变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com