练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图一次函数y1=-x-2与y2=x-4的图象相交于点A．

    （1）求点A的坐标；

    （2）若一次函数y1=-x-2与y2=x-4的图象与x轴分别相交于点B、C，求△ABC的面积．

    （3）结合图象，直接写出y1＞y2时x的取值范围．

    【答案】（1）（1，-3）；（2）9；（3）y1＞y2时x的取值范围是x＜1

    【解析】

    （1）解两函数的解析式组成的方程组，求出方程组的解，即可得出答案；

    （2）求出B、C的坐标，再根据三角形的面积公式求出即可；

    （3）根据函数的图象和A点的坐标得出即可．

    （1）解方程组得：，

    以A点的坐标是（1，-3）；

    （2）函数y=-x-2中当y=0时，x=-2，

    函数y=x-4中，当y=0时，x=4，

    即OB=2，OC=4，

    所以BC=2+4=6，

    ∵A（1，-3），

    ∴△ABC的面积是=9；

    （3）y1＞y2时x的取值范围是x＜1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】抛物线y=（x﹣3）（x+1）与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．

    （1）求点B及点D的坐标．

    （2）连结BD，CD，抛物线的对称轴与x轴交于点E．

    ①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．

    ②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A、B在数轴上分别表示数a，b．若A、B两点间的距离记为d，则d和a，b之间的数量关系是d=|a-b|.

    (1)数轴上有理数x与有理数－2所对应两点之间的距离可以表示为______；

    (2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离；

    若|x+6|= |x -2|，则x=______；

    (3)若a=1，b=-2，将数轴折叠，使得A点与﹣7表示的点重合，则B点与数______表示的点P重合；

    (4)若数轴上M、N两点之间的距离为11(M在N的左侧)，且M、N两点经过(3)中折叠后互相重合，则M、N两点表示的数分别是：M：_____， N：_______；

    (5)在题(3)的条件下，点A为定点，点B、P为动点，若移动点B、P中一点后，能否使相邻两点间距离相等？若能，请写出移动方案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在学习完《有理数》后，小奇对运算产生了浓厚的兴趣．借助有理数的运算，定义了一种新运算“⊕”，规则如下：a⊕b＝a×b+2×a．

    （1）求2⊕（﹣1）的值；

    （2）求﹣3⊕（﹣4⊕）的值；

    （3）试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律？请写出你的探究过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC、BD交于点O，AE平分交BC于点E，且， ，连接OE．下列结论：①；②SABCD＝ABAC；③OB＝AB；④，成立的个数有_________个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A是抛物线与x轴正半轴的交点，点B在抛物线上，其横坐标为2，直线AB与y轴交于点点M、P在线段AC上不含端点，点Q在抛物线上，且MQ平行于x轴，PQ平行于y轴设点P横坐标为m．

    （1）求直线AB所对应的函数表达式．

    （2）用含m的代数式表示线段PQ的长．

    （3）以PQ、QM为邻边作矩形PQMN，求矩形PQMN的周长为9时m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料并解决有关问题：

    我们知道：|x|＝．现在我们可以用这一结论来化简含有绝对值的代数式，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x﹣2|时，可令x+1＝0和x﹣2＝0，分别求得x＝﹣1，x＝2（称﹣1，2分别为|x+1|与|x﹣2|的零点值）．在实数范围内，零点值x＝﹣1和，x＝2可将全体实数分成不重复且不遗漏的如下3种情况：

    ①x＜﹣1；②﹣1≤x＜2；③x≥2．

    从而化简代数式|x+1|+|x﹣2|可分以下3种情况：

    ①当x＜﹣1时，原式＝﹣（x+1）﹣（x﹣2）＝﹣2x+1；

    ②当﹣1≤x＜2时，原式＝x+1﹣（x﹣2）＝3；

    ③当x≥2时，原式＝x+1+x﹣2＝2x﹣1．综上讨论，原式＝．

    通过以上阅读，请你解决以下问题：

    （1）化简代数式|x+2|+|x﹣4|．

    （2）求|x﹣1|﹣4|x+1|的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，Rt△ABC的直角边AC在x轴上，∠ACB=90°，AC=1，反比例函数（k＞0）的图象经过BC边的中点D（3，1）．

    （1）求这个反比例函数的表达式；

    （2）若△ABC与△EFG成中心对称，且△EFG的边FG在y轴的正半轴上，点E在这个函数的图象上．

    ①求OF的长；

    ②连接AF，BE，证明四边形ABEF是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，反比例函数的图像经过第二象限内的点，轴于点，的面积为2.若直线经过点，并且经过反比例函数的图像上另一点.

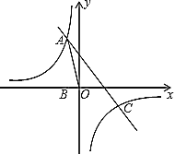
    （1）求反比例函数与直线的解析式；

    （2）连接，求的面积；

    （3）不等式的解集为_________

    （4）若在图像上，且满足，则的取值范围是_________.

    查看答案和解析>>

    同步练习册答案