Question

13．如图，在平面直角坐标系中，矩形ABCD的顶点A与坐标原点O重合，B（4，0），D（0，3），点E从点A出发，沿射线AB移动，以CE为直径作⊙M，点F为⊙M与射线DB的公共点，连接EF、CF，过点E作EG⊥EF，EG与⊙M相交于点G，连接CG．
（1）试说明四边形EFCG是矩形；
（2）求tan∠CEG的值；
（3）当⊙M与射线DB相切时，点E停止移动，在点E移动的过程中：
①点M运动的路径长$\frac{25}{8}$；点G运动的路径长$\frac{15}{4}$；
②矩形EFCG的面积最小值是$\frac{108}{25}$；
③当△BCG成为等腰三角形时，直接写出点G坐标（$\frac{41}{8}$，$\frac{3}{2}$）．

Answer 1

分析 （1）根据三个角是直角的四边形是矩形即可判断．
（2）只要证明∠CEG=∠ADB即可解决问题；
（3）①根据圆周角定理和矩形的性质可证到∠GDC=∠FDE=定值，从而得到点G的移动的路线是线段，只需找到点G的起点与终点，求出该线段的长度即可；再判断出M的移动路线是线段M'M''；
②欲求矩形EFCG面积的最小值，由题意可知当EC最小时，面积最小，求出EG、CG即可解决问题．
③先判断出BG=CG时，点F是矩形ABCD的对角线BD中点，利用三角形的中位线求出FH，再用勾股定理计算即可．

解答 解：（1）证明：∵CE为⊙O的直径，
∴∠CFE=∠CGE=90°，
∵EG⊥EF，
∴∠FEG=90°，
∴∠CFE=∠CGE=∠FEG=90°，
∴四边形EFCG是矩形．

（2）由（1）知四边形EFCG是矩形．
∴CF∥EG，
∴∠CEG=∠ECF，
∵∠ECF=∠EBF，
∴∠CEG=∠EBF，
在Rt△ABD中，AD=3，AB=4，
∴tan∠ABD=$\frac{AD}{AB}$，
∴tan∠CEG=$\frac{3}{4}$；

（3）①∵∠GBC=∠FBE=定值，点G的起点为B，终点为G″，如图2所示，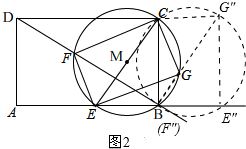

∴点G的移动路线是线段BG″，
∵∠G″BC=∠DBA，∠BCG″=∠A=90°，
∴△BCG″∽△BAD．
∴$\frac{BC}{AB}$=$\frac{BG″}{DB}$=$\frac{CG″}{AD}$．
∴$\frac{3}{4}$=$\frac{BG″}{5}$=$\frac{CG″}{3}$，
∴BG″=$\frac{15}{4}$，CG''=$\frac{9}{4}$，
∴点G移动路线的长为 $\frac{15}{4}$，
∵点M是以CE为直径的圆的圆心，点M的起点是M'，终点是M''，如图2-1所示，且M'M''∥AB，
∴点M的移动路线为线段M'M''，
∵点M'，M''是AC，CE''的中点，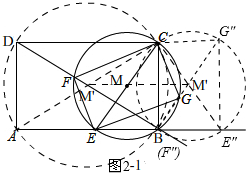

∴M'M''=$\frac{1}{2}$AB+$\frac{1}{2}$CG''=2+$\frac{9}{8}$=$\frac{25}{8}$，
点M运动的路径长为$\frac{25}{8}$，
故答案分别为$\frac{25}{8}$，$\frac{15}{4}$．

②∵tan∠CEG=$\frac{3}{4}$，是定值，
∴∠CEG的大小不变，
∴CE最短时，矩形CFEG的面积最小，此时EC=3，
∴设CG=3k，EG=4k，则有25k²=9，
∴k=$\frac{3}{5}$，CG=$\frac{9}{5}$，EG=$\frac{12}{5}$，
∴矩形EFCG的面积最小值=CG•EG=$\frac{108}{25}$，
故答案为$\frac{108}{25}$．

③如图3，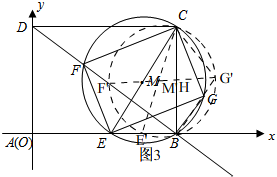
由运动知，点G始终是劣弧 $\widehat{BC}$上，
∵△BCG成为等腰三角形，
∴只有BG=CG，
∵四边形E'F'CG'是矩形，
∴点F'是BD中点，
∵F'G'∥CD，
∴F'H=$\frac{1}{2}$AB=2，M'H=$\frac{1}{2}$BE'，
设⊙M'的半径为r，则M'H=2-r，
∴BE'=2（2-r），
在Rt△BCE'中，CE'=2r，BC=3，
根据勾股定理得，（2r）²-[2（2-r）]²=9，
∴r=$\frac{25}{16}$，
∵F是BD中点，
∴F（2，$\frac{3}{2}$），
∴G'（2+2×$\frac{25}{16}$，$\frac{3}{2}$），
∴G'（ $\frac{41}{8}$，$\frac{3}{2}$）．
故答案为（$\frac{41}{8}$，$\frac{3}{2}$）．

点评 此题是圆的综合题，主要考查考查了矩形的判定与性质、相似三角形的判定与性质、圆周角定理、直角三角形斜边上的中线等于斜边的一半、垂线段定理等知识，考查了动点的移动的路线长，综合性较强．而发现∠CBG=∠ABD及∠FCE=∠ABD是解决本题的关键．判断出点F是线段BD中点是难点．