
【题目】我们定义:在平面直角坐标系![]() 中,经过点
中,经过点![]() ,且平行于直线
,且平行于直线![]() 或
或![]() ,叫过该点的“二维线”.例如,点
,叫过该点的“二维线”.例如,点![]() 的“二维线”有:
的“二维线”有:![]() ,
,![]() .
.
(1)写出点![]() 的“二维线”______;
的“二维线”______;
(2)若点![]() 的“二维线”是
的“二维线”是![]() ,
,![]() ,求
,求![]() 、
、![]() 的值;
的值;
(3)若反比例函数![]() 图像上的一个点
图像上的一个点![]() 有一条“二维线”是
有一条“二维线”是![]() ,求
,求![]() 点
点![]() 的另一条“二维线”.
的另一条“二维线”.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据“二维线”的定义和待定系数法解答即可;
(2)把点![]() 分别代入两个一次函数关系式可得关于m、n的方程组,解方程组即得结果;
分别代入两个一次函数关系式可得关于m、n的方程组,解方程组即得结果;
(3)把点![]() 分别代入反比例函数和一次函数关系式可得关于m、n的方程组,解方程组即可求出m、n的值,再根据“二维线”的定义即可求得结果.
分别代入反比例函数和一次函数关系式可得关于m、n的方程组,解方程组即可求出m、n的值,再根据“二维线”的定义即可求得结果.
解:(1)设点![]() 的“二维线”是:
的“二维线”是:![]() 与
与![]() ,
,
把点![]() 分别代入,得
分别代入,得![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
∴点![]() 的“二维线”是:
的“二维线”是:![]() ,
,![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)根据题意,得:![]() ,解得:
,解得:![]() ,
,![]() ;
;
(3)由题意,得: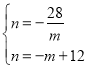 ,解得:
,解得: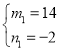 ,
,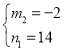 ,
,
设点![]() 的另一条“二维线”是
的另一条“二维线”是![]() ,
,
当m=14,n=﹣2时,﹣2=14+a,解得:a=﹣16;
当m=﹣2,n=14时,14=﹣2+a,解得:a=16;
∴点![]() 的另一条“二维线”是
的另一条“二维线”是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边
ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边![]() CDE.
CDE.
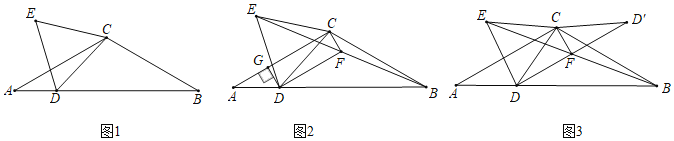
(1)如图1,若∠CDB=45°,AB=6,求等边![]() CDE的边长;
CDE的边长;
(2)如图2,点D在AB边上移动过程中,连接BE,取BE的中点F,连接CF,DF,过点D作DG⊥AC于点G.
①求证:CF⊥DF;
②如图3,将![]() CFD沿CF翻折得
CFD沿CF翻折得![]() CF
CF![]() ,连接B
,连接B![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的函数表达式为
的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() 以
以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ;以
;以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ;以
;以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ;······按此做法进行下去,其中弧
;······按此做法进行下去,其中弧![]() 的长________________.
的长________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意外创伤随时可能发生,急救是否及时、妥善,直接关系到病人的安危.为普及急救科普知识,提高学生的急救意识与现场急救能力,某校开展了急救知识进校园培训活动.为了解七、八年级学生(七、八年级各有600名学生)的培训效果,该校举行了相关的急救知识竞赛.现从两个年级各随机抽取20名学生的急救知识竞赛成绩(百.分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,78,81,72,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 | |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 | c |
八年级 | 78 | d | 80.5 |
应用数据:
(1)由上表填空:a= ;b= ;c= ;d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在80分及以上的共有多少人?
(3)你认为哪个年级的学生对急救知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
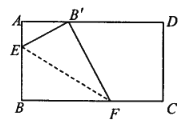
【题目】如图,矩形纸片![]() 中,
中,![]() ,
,![]() .现将纸片折叠,折痕与矩形
.现将纸片折叠,折痕与矩形![]() 、
、![]() 边的交点分别为
边的交点分别为![]() 、
、![]() .折叠后点
.折叠后点![]() 的对应点
的对应点![]() 始终在
始终在![]() 边上.若折痕
边上.若折痕![]() 始终与边
始终与边![]() ,
,![]() 有交点,则点
有交点,则点![]() 运动的最大距离是______.
运动的最大距离是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax.
(1)二次函数图象的对称轴是直线x= ;
(2)当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;
(3)若a<0,对于二次函数图象上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2,请结合函数图象,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
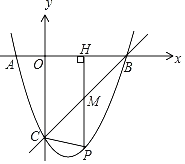
【题目】如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C.
(1)求抛物线的解析式;
(2)点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.
①线段PM是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com