
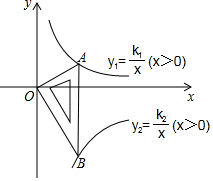
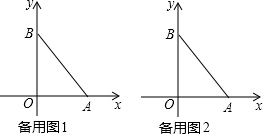
 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$.
如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,顶点B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,∠ABO=30°,则$\frac{k_1}{k_2}$=-$\frac{1}{3}$. 分析 设AC=a,则OA=2a,OC=$\sqrt{3}$a,根据直角三角形30°角的性质和勾股定理分别计算点A和B的坐标,写出A和B两点的坐标,代入解析式求出k1和k2的值,相比即可.
解答 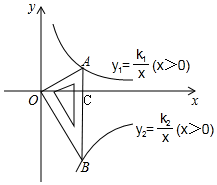 解:如图,Rt△AOB中,∠B=30°,∠AOB=90°,
解:如图,Rt△AOB中,∠B=30°,∠AOB=90°,
∴∠OAC=60°,
∵AB⊥OC,
∴∠ACO=90°,
∴∠AOC=30°,
设AC=a,则OA=2a,OC=$\sqrt{3}$a,
∴A($\sqrt{3}$a,a),
∵A在函数y1=$\frac{k_1}{x}$(x>0)的图象上,
∴k1=$\sqrt{3}$a•a=$\sqrt{3}{a}^{2}$,
Rt△BOC中,OB=2OC=2$\sqrt{3}$a,
∴BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=3a,
∴B($\sqrt{3}$a,-3a),
∵B在函数y2=$\frac{k_2}{x}$(x>0)的图象上,
∴k2=-3a$•\sqrt{3}$a=-3$\sqrt{3}{a}^{2}$,
∴$\frac{k_1}{k_2}$=-$\frac{1}{3}$;
故答案为:-$\frac{1}{3}$.
点评 本题考查了反比例函数图象上点的特征、直角三角形30°的性质,熟练掌握直角三角形30°角所对的直角边是斜边的一半,正确写出A、B两点的坐标是关键.


科目:初中数学 来源: 题型:解答题
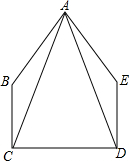 如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
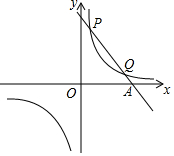 已知一次函数y=k1x+b与反比例函数y=$\frac{k_2}{x}$的图象交于第一象限内的P($\frac{1}{2}$,8),Q(4,m)两点,与x轴交于A点.
已知一次函数y=k1x+b与反比例函数y=$\frac{k_2}{x}$的图象交于第一象限内的P($\frac{1}{2}$,8),Q(4,m)两点,与x轴交于A点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
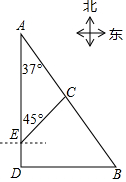 如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | )$\frac{1}{9}$ | B. | )$\frac{1}{6}$ | C. | )$\frac{1}{4}$ | D. | )$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
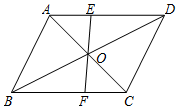 如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
如图,EF过?ABCD对角线的交点O,交AD于E,交BC于F,若?ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )| A. | 14 | B. | 13 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
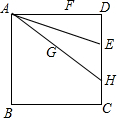 如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$.
如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com