
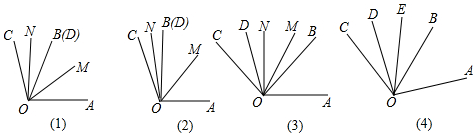
分析 (1)利用角平分线的性质即可得出∠MON=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠BOC,进而求出即可;
(2))设∠BOD=γ,而∠MOD=$\frac{∠AOD}{2}$=$\frac{α+γ}{2}$,∠NOB=$\frac{∠COB}{2}$=$\frac{β+γ}{2}$,进而得出即可;
(3)利用已知表示出∠COE和∠AOD,进而得出答案.
解答 解:(1)∵OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β,
α=90゜,β=30゜,
∴∠MON=$\frac{1}{2}$α+$\frac{1}{2}$β=60°;
故答案为:60°;
(2)设∠BOD=γ,
∵∠MOD=$\frac{∠AOD}{2}$=$\frac{α+γ}{2}$,∠NOB=$\frac{∠COB}{2}$=$\frac{β+γ}{2}$,
∴∠MON=∠MOD+∠NOB-∠DOB=$\frac{β+γ}{2}$+$\frac{α+γ}{2}$-γ=$\frac{α+β}{2}$;
(3)设运动时间为t秒,则∠DOB=3t-t=2t,∠DOE=$\frac{1}{2}$∠DOB=t,
∴∠COE=β+t.∠AOD=α+2t,
又∵α=2β,
∴∠AOD=2β+2t=2(β+t).
∴$\frac{∠COE}{AOD}$=$\frac{1}{2}$,
∴∠COE=2∠AOD.
点评 此题主要考查了角的计算,正确根据角平分线的性质应用α,β表示角是解题关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
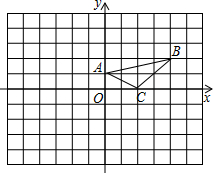 如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
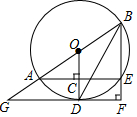 已知,如图,AB是⊙O的直径,AE是⊙O的弦,过点O作⊙O的半径OD⊥AE于点C,延长交⊙O于点D,连BE并延长,过点D作DF⊥BE于点F,交BA的延长线于点G.
已知,如图,AB是⊙O的直径,AE是⊙O的弦,过点O作⊙O的半径OD⊥AE于点C,延长交⊙O于点D,连BE并延长,过点D作DF⊥BE于点F,交BA的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一个边长分别为4、8的矩形纸片ABCD折叠,使点C与点A重合(AB=4,BC=8),则折痕EF的长度为( )
如图,将一个边长分别为4、8的矩形纸片ABCD折叠,使点C与点A重合(AB=4,BC=8),则折痕EF的长度为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
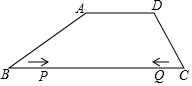 如图,四边形ABCD中,AD∥BC,AD=5cm,AB=$\sqrt{46}$cm,BC=13cm,DC=$\sqrt{30}$cm.在BC上有动点P、Q,P从B到C,以2cm/s的速度运动,Q从C到B,以1cm/s的速度同时开始运动,当P到达终点时,Q也立刻停止,设运动的时间为t(s).
如图,四边形ABCD中,AD∥BC,AD=5cm,AB=$\sqrt{46}$cm,BC=13cm,DC=$\sqrt{30}$cm.在BC上有动点P、Q,P从B到C,以2cm/s的速度运动,Q从C到B,以1cm/s的速度同时开始运动,当P到达终点时,Q也立刻停止,设运动的时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com