【题目】下列命题:(1)如果 
，那么点 
是线段 
的中点;(2)相等的两个角是对顶角;(3)直角三角形的两个锐角互余;(4)同位角相等;(5)两点之间，直线最短.其中真命题的个数有( )
A.1 个B.2 个C.3 个D.4 个
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】将一副三角板中的两块直角三角形的直角顶点0按图1方式叠放在一起(其中∠C＝30°，∠CDO＝60°；∠OAB＝∠OBA＝45°).△COD绕着点O顺时针旋转一周，旋转的速度为每秒10°，若旋转时间为t秒，请回答下列问题：(请直接写出答案)
(1)当0＜t＜9时(如图2)，∠BOC与∠AOD有何数量关系
(2)当t为何值时，边OA∥CD？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在ABCD中，点E、F分别在AD、BC上，EF与BD相交于点O，AE=CF．
（1）求证：OE=OF；
（2）连接BE、DF，若BD平分∠EBF，试判断四边形EBFD的形状，并给予证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图，在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，且MN=DM．设OM=a，请你利用基本活动经验直接写出点N的坐标______（用含a的代数式表示）；
（2）如果（1）的条件去掉“且MN=DM”，加上“交∠CBE的平分线与点N”，如图，求证：MD=MN．如何突破这种定势，获得问题的解决，请你写出你的证明过程．
（3）在（2）的条件下，如图，请你继续探索：连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，请你指出正确的结论，并给出证明．
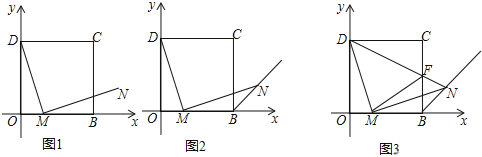
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BD=DG．
下列结论：（1）DE=DF；（2）∠B=∠DGF； （3）AB＜AF+FG；（4）若△ABD和△ADG的面积分别是50和38，则△DFG的面积是8．其中一定正确的有（ ）
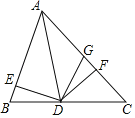
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC的三条角平分线相交于点I，过点I作DI⊥IC，交AC于点D.
(1)如图①，求证：∠AIB＝∠ADI；
(2)如图②，延长BI，交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系，并说明理由；
②若∠BAC＝70°，求∠F的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：
甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．
乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形．
根据两人的作法可判断
A．甲正确，乙错误 B．乙正确，甲错误 C．甲、乙均正确 D．甲、乙均错误
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂计划生产
两种产品共10件，其生产成本和销售价如下表所示：
产品 |
|
|
成本（万元/件） | 3 | 5 |
售价（万元/件） | 4 | 7 |
（1）若工厂计划获利14万元，则应分别生产两种产品多少件？
（2）若工厂投入资金不多于44万元，且获利不少于14万元，则工厂有哪些生产方案？
（3）在第（2）的条件下，哪种方案获利最大；最大利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
