
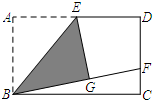
 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )| A. | $\frac{13}{3}$ | B. | $\frac{25}{3}$ | C. | 10 | D. | 12 |
分析 过点E作EM⊥BC于M,交BF于N,根据矩形的性质得到∠A=∠ABC=90°,AD=BC,AE=BM=$\frac{1}{2}$AD=2,由折叠的性质得到AE=GE=2,∠EGN=∠A=90°,根据全等三角形的性质得到NG=NM,根据勾股定理得到EN=$\frac{13}{6}$,NM=$\frac{5}{6}$,根据三角形的中位线的性质得到CF=2NM=$\frac{5}{3}$,于是得到结论.
解答 解:过点E作EM⊥BC于M,交BF于N,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,
∴四边形ABME是矩形,
∴AE=BM=$\frac{1}{2}$AD=2,
由折叠的性质得:AE=GE=2,∠EGN=∠A=90°,
∴EG=BM=2,
∵∠ENG=∠BNM,
在△ENG与△BNM中,$\left\{\begin{array}{l}{∠EGN=∠BMN=90°}\\{∠ENG=∠BNM}\\{EG=BM}\end{array}\right.$
∴△ENG≌△BNM(AAS),
∴NG=NM,
∴EN2=NG2+EG2,
∴EN2=22+(3-EN)2,
∴EN=$\frac{13}{6}$,
∴BN=EN=$\frac{13}{6}$,
∴NM=$\frac{5}{6}$,
∵E是AD的中点,
∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BF=2BN=$\frac{13}{3}$,
∴CF=2NM=$\frac{5}{3}$,
∴△BCF的周长=10,
故选C.
点评 此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
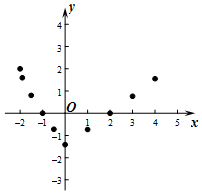 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?| x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
| y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )| A. | 16$\sqrt{3}$ | B. | 24 | C. | 12$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
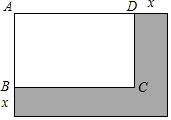 如图,矩形ABCD的长AD=5cm,宽AB=3cm,长和宽都增加xcm,那么面积增加ycm2.
如图,矩形ABCD的长AD=5cm,宽AB=3cm,长和宽都增加xcm,那么面积增加ycm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com