
【题目】小慧同学根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 .
(2)列表,找出y与x的几组对应值.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 2 | b | 0 | 1 | 2 | … |
其中,b= .
(3)在所给的平面直角坐标系xoy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)请根据你画出的函数图象,完成:当x=﹣5时.y= .当2012≤|y|≤2019时,x的取值范围是 .
【答案】(1)任意实数;(2)b=1;(3)见解析;(4)y=6;﹣2018≤x≤﹣2011或2013≤x≤2020
【解析】
(1)根据一次函数的性质即可得出结论;
(2)把x=0代入函数解析式,求出y的值即可;
(3)在坐标系内描出各点,再顺次连接即可;
(4)根据函数图象即可得出结论.
(1)∵x无论为何值,函数均有意义,
∴x为任意实数.
故答案为:任意实数;
(2)∵当x=0时,y=|0﹣1|=1,
∴b=1.
故答案为:1;
(3)如图所示:
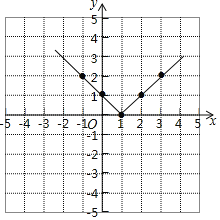
(4)当x=﹣5时.y=|﹣5﹣1|=6.
当y=2012时,|x﹣1|=2012,解得x=2013或x=﹣2011,
当y=2019时,|x﹣1|=2019,解得x=2020或x=﹣2018,
由函数图象可知,当2012≤|y|≤2019时,x的取值范围是﹣2018≤x≤﹣2011或2013≤x≤2020,


科目:初中数学 来源: 题型:
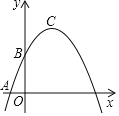
【题目】在平面直角坐标系xOy中(如图).已知抛物线y=﹣![]() x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0,![]() ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)求这条抛物线的表达式;
(2)求线段CD的长;
(3)将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
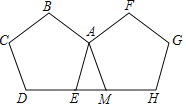
【题目】如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一直线上,且有一个公共顶点A,若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合,则x的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
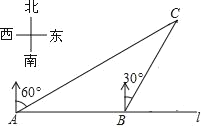
【题目】如图,在一笔直的海岸线l上有相距2km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离为多少千米?(参考数据:![]() ≈1.732,结果保留小数点后一位)
≈1.732,结果保留小数点后一位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图中的曲线是反比例函数![]() 为常数)图象的一支.
为常数)图象的一支.
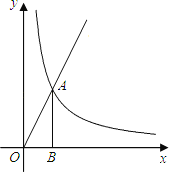
(1)这个反比例函数图象的另一支在第几象限?常数![]() 的取值范围是什么?
的取值范围是什么?
(2)若该函数的图象与正比例函数![]() 的图象在第一象限内的交点为
的图象在第一象限内的交点为![]() ,过
,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,当
,当![]() 的面积为4时,求点
的面积为4时,求点![]() 的坐标及反比例函数的关系式.
的坐标及反比例函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
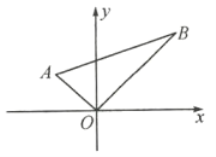
【题目】在平面直角坐标系![]() 中,
中,![]() 的位置如图所示,已知
的位置如图所示,已知![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求图像经过![]() 、
、![]() 、
、![]() 三点的二次函数的解析式和这个函数图像的顶点坐标.
三点的二次函数的解析式和这个函数图像的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )

A. 1 m B. 2 m C. 3 m D. 6 m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com