
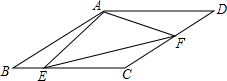
 如图,AB∥CD,AD∥BC,点E、F分别是线段BC和CD上的动点,在两点运动到某一位置时,恰好使得∠AEF=∠AFE,此时量得∠BAE=15°,∠FEC=12°,∠DAF=25°,则∠EFC=22°.
如图,AB∥CD,AD∥BC,点E、F分别是线段BC和CD上的动点,在两点运动到某一位置时,恰好使得∠AEF=∠AFE,此时量得∠BAE=15°,∠FEC=12°,∠DAF=25°,则∠EFC=22°. 分析 设∠EAF=x,得到∠AEF=∠AFE=$\frac{180°-x}{2}$,由于AD∥BC,于是得到∠AEB=∠EAD=x+25°,根据∠AEB+∠AEF+∠FEC=180°,列方程得到∠BAD=146°,证得四边形ABCD是平行四边形,得到∠C=∠BAD=146°,根据三角形的内角和得到结果.
解答 解:设∠EAF=x,
∴∠AEF=∠AFE=$\frac{180°-x}{2}$,
∵AD∥BC,
∴∠AEB=∠EAD=x+25°,
∵∠AEB+∠AEF+∠FEC=180°,
∴x+25°+$\frac{180°-x}{2}$+12°=180°
解得:x=106°,
∴∠BAD=146°,
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴∠C=∠BAD=146°,
∴∠EFC=180°-146°-12°=22°,
故答案为:22°
点评 本题考查了平行线的性质,等腰三角形的性质,三角形的内角和,平行四边形的判定,熟练掌握性质定理是解题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:填空题
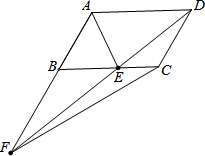 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=2cm,则△CEF面积是$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
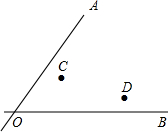 如图:点C,D分别表示两所大学,AO,BO表示两条公路,现计划修建一个超市,希望超市到两所大学的距离相等,到两条公路的距离也相等,请你找出超市所在的位置.(只用直尺和圆规)
如图:点C,D分别表示两所大学,AO,BO表示两条公路,现计划修建一个超市,希望超市到两所大学的距离相等,到两条公路的距离也相等,请你找出超市所在的位置.(只用直尺和圆规)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com