
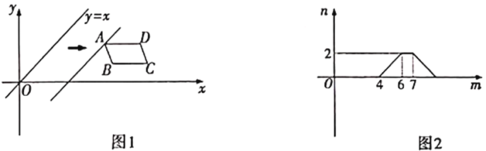
【题目】如图1,在平面直角坐标系中,![]() 在第一象限,且
在第一象限,且![]() 轴.直线
轴.直线![]() 从原点
从原点![]() 出发沿
出发沿![]() 轴正方向平移.在平移过程中,直线被
轴正方向平移.在平移过程中,直线被![]() 截得的线段长度
截得的线段长度![]() 与直线在
与直线在![]() 轴上平移的距离
轴上平移的距离![]() 的函数图象如图2所示.那么
的函数图象如图2所示.那么![]() 的面积为( )
的面积为( )
A.3B.![]() C.6D.
C.6D.![]()
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

查看答案和解析>>
科目:初中数学 来源: 题型:
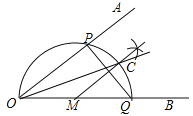
【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 ![]() 于点C;
于点C;
步骤3:画射线OC.
则下列判断:①![]() =
=![]() ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年甘肃在国际知名旅游指南《孤独星球》亚洲最佳旅游地排名第一,截至2020年1月,甘肃省已有五家国家5A级旅游景区,分别为A:嘉峪关文物景区;B:平凉崆峒山风景名胜区;C:天水麦积山景区;D:敦煌鸣沙月牙泉景区:E:张掖七彩舟霞景区,张帆同学与父母计划在暑假期间从中选择部分景区游玩.
(1)张帆一家选择E:张掖七彩丹霞景区的概率是多少?
(2)若张帆一家选择了E:张掖七彩丹霞景区,他们再从![]() ,
,![]() ,
,![]() ,
,![]() 四个景区中任选两个景区去旅游,求选
四个景区中任选两个景区去旅游,求选![]() ,
,![]() 两个景区的概率(要求画树状图或列表求概率).
两个景区的概率(要求画树状图或列表求概率).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系![]() 中,等腰
中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,
轴上,![]() ,顶点
,顶点![]() 在
在![]() 的正半轴上,
的正半轴上,![]() ,一动点
,一动点![]() 从
从![]() 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿![]() 向左运动,到达
向左运动,到达![]() 的中点停止.另一动点
的中点停止.另一动点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向左运动,到达点
向左运动,到达点![]() 停止.已知点
停止.已知点![]() 、
、![]() 同时出发,以
同时出发,以![]() 为边作正方形
为边作正方形![]() ,使正方形
,使正方形![]() 和
和![]() 在
在![]() 的同侧.设运动的时间为
的同侧.设运动的时间为![]() 秒(
秒(![]() ).
).
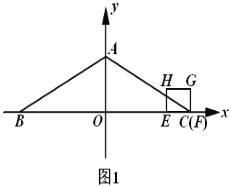
(1)当点![]() 落在
落在![]() 边上时,求
边上时,求![]() 的值;
的值;
(2)设正方形![]() 与
与![]() 重叠面积为
重叠面积为![]() ,请问是存在
,请问是存在![]() 值,使得
值,使得![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由;
值;若不存在,请说明理由;
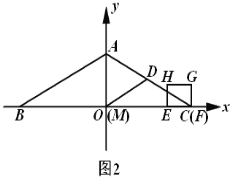
(3)如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() ,当点
,当点![]() 、
、![]() 开始运动时,点
开始运动时,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 运动,到达点
运动,到达点![]() 停止运动.请问在点
停止运动.请问在点![]() 的整个运动过程中,点
的整个运动过程中,点![]() 可能在正方形
可能在正方形![]() 内(含边界)吗?如果可能,求出点
内(含边界)吗?如果可能,求出点![]() 在正方形
在正方形![]() 内(含边界)的时长;若不可能,请说明理由.
内(含边界)的时长;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
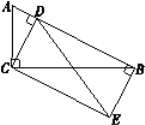
【题目】如图,在Rt△ABC中,![]() ,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
(1)求证:四边形CDBE为矩形;
(2)若AC=2,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() .
.![]() 轴,且与直线
轴,且与直线![]() 交于点
交于点![]() ,
,![]() 轴并交
轴并交![]() 轴于点
轴于点![]() ,点
,点![]() 是折线
是折线![]() 上一点.设过点
上一点.设过点![]() ,
,![]() 的直线为
的直线为![]() .
.
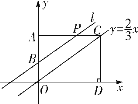
(1)点![]() 的坐标为________;若
的坐标为________;若![]() 所在的直线
所在的直线![]() 的函数值随
的函数值随![]() 的增大而减小,则
的增大而减小,则![]() 的取值范围是________;
的取值范围是________;
(2)当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)若![]() 与线段
与线段![]() 有交点,设该交点为
有交点,设该交点为![]() ,是否存在
,是否存在![]() 的情况?若存在,求点
的情况?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com