
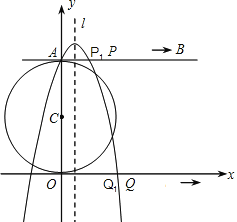
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
【答案】(1)y=![]() , l:x=
, l:x=![]() ;(2)t=2时,PQ与⊙C相切,P(2,8),Q(8,0);(3)N(1,7),理由见解析.
;(2)t=2时,PQ与⊙C相切,P(2,8),Q(8,0);(3)N(1,7),理由见解析.
【解析】
(1)先求出t=1时P1,Q1的坐标,然后用待定系数法即可得出抛物线的解析式,进而可求出对称轴l的解析式;
(2)当直线PQ与圆C相切时,连接CP,CQ,根据平行线的性质、角平分线的性质和三角形的内角和可得∠PCQ=90°,则有Rt△CMP∽Rt△QMC(M为PQ与圆C的切点),然后根据相似三角形的性质即可求出t的值;
(3)本题是典型的“将军饮马”问题,解题的关键是确定N的位置,可先利用待定系数法求出此时抛物线的解析式,然后作出P点关于直线l的对称点P′的坐标,连接P′Q,那么P′Q与直线l的交点即为所求的N点,至此只要求出直线P′Q的解析式,即可求出N点的坐标,问题即得解决.
解:(1)当t=1时,AP1=1,OQ1=4,则A、P1、Q1的坐标分别为A(0,8)、P1(1,8)、Q1(4,0),
设所求抛物线解析式为y=ax2+bx+c,则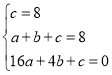 ,解得:
,解得: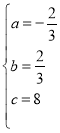
∴抛物线的解析式为y=![]() ,对称轴为直线l:x=
,对称轴为直线l:x=![]() ;
;
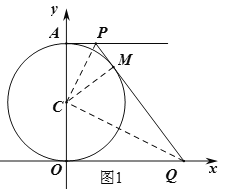
(2)设PQ与⊙C相切于点M,如图1,连接CP、CM、CQ,则PA=PM=t,QO=QM=4t,
∵CP、CQ分别平分∠APQ和∠OQP,∴![]() ,
,![]() ,
,
∵∠APQ+∠OQP=180°,∴∠CPQ+∠CQP=90°,
∴∠PCQ=![]() =90°,
=90°,
∵CM⊥PQ,∴可得Rt△CMP∽Rt△QMC,
∴![]() ,即
,即![]() ,∴t=±2,
,∴t=±2,
由于时间t只能取正数,所以t=2,即当运动时间t=2秒时,PQ与⊙C相切.
此时:P(2,8),Q(8,0);
(3)∵A(0,8),P(2,8),Q(8,0),∴设此时抛物线的解析式为![]() ,
,
把A,P,Q代入,得: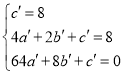 ,解得:
,解得: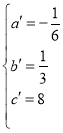 ,
,
∴抛物线的解析式为:y=![]() ,此时抛物线的对称轴为直线l:x=1,
,此时抛物线的对称轴为直线l:x=1,
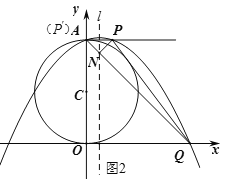
作点P关于直线l的对称点P',如图2,则P'(0,8),即为点A,设P'Q与直线x=1交于点N,则此时NP+NQ最小,
∵P'(0,8),Q(8,0),∴直线P'Q的解析式为:y=﹣x+8,当x=1时,y=﹣1+8=7.
因此N点的坐标为(1,7).


科目:初中数学 来源: 题型:
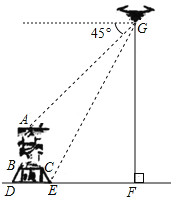
【题目】为了测量重庆有名的观景点南山大金鹰的大致高度,小南同学使用的无人机进行观察,当无人机与大金鹰侧面在同一平面,且距离水平面垂直高度GF为100米时,小南调整摄像头方向,当俯角为45°时,恰好可以拍摄到金鹰的头顶A点;当俯角为63°时,恰好可以拍摄到金鹰底座点E.已知大金鹰是雄踞在一人造石台上,石台侧面CE长12.5米,坡度为1:0.75,石台上方BC长10米,头部A点位于BC中点正上方.则金鹰自身高度约( )米.(结果保留一位小数,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
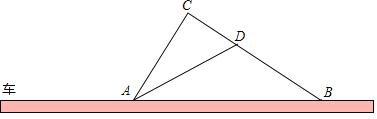
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
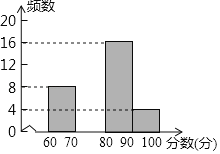
请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学. 学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
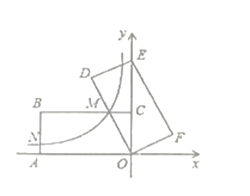
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
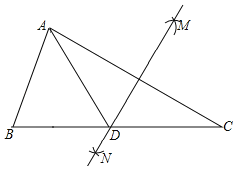
【题目】如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于![]() AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=4,∠C=30°,则△ACD的面积为( )
AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=4,∠C=30°,则△ACD的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.13
D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com