
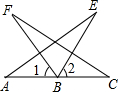
 如图,B是AC中点,∠F=∠E,∠1=∠2.证明:AE=CF.
如图,B是AC中点,∠F=∠E,∠1=∠2.证明:AE=CF.  备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
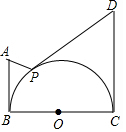 (1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.
(1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
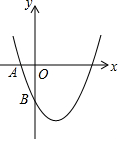 如图,函数y=x2-2x-3与坐标轴交于A、B两点,问抛物线上是否存在点C使四边形ABCO为平行四边形,若存在,求出点C的坐标;若不存在,说明理由.
如图,函数y=x2-2x-3与坐标轴交于A、B两点,问抛物线上是否存在点C使四边形ABCO为平行四边形,若存在,求出点C的坐标;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
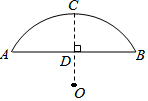 有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD,长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?
有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD,长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
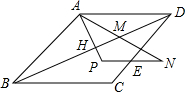 如图,E为菱形ABCD的边CD上任意点,将CE绕点E旋转一定角度后与AD平行.
如图,E为菱形ABCD的边CD上任意点,将CE绕点E旋转一定角度后与AD平行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com