
【题目】(感知)小亮遇到了这样一道题:已知如图在![]() 中,
中,![]() 在
在![]() 上,
上,![]() 在
在![]() 的延长上,
的延长上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
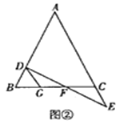
小亮仔细分析了题中的已知条件后,如图②过![]() 点作
点作![]() 交
交![]() 于
于![]() ,进而解决了该问题.(不需要证明)
,进而解决了该问题.(不需要证明)
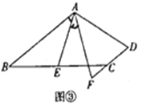
(探究)如图③,在四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,试探究线段
,试探究线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(应用)如图③,在正方形![]() 中,
中,![]() 为
为![]() 边的中点,
边的中点,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 边上的点,若
边上的点,若![]() =1,
=1,![]() =
=![]() ,∠
,∠![]() =90°,则
=90°,则![]() 的长为 .
的长为 .

【答案】探究:![]() ;应用:
;应用:![]() .
.
【解析】
探究:分别延长DC、AE,交于点G,根据已知条件可以得到△ABE≌△GCE,由此得到AB=CG,由∠BAE=∠EAF,等量代换可证∠CGE=∠EAF,进而得到AF=GF,即可得出结论;
应用:分别延长FB、GE,交于点H,根据已知条件可以得到△AEG≌△BEH,由此得到AG=BH,GE=HE,然后利用三线合一的性质得到FG=FH,即可求出GF.
解:探究:AB=AF+CF;
证明:如图,分别延长DC、AE,交于点G,

∵AB∥DC,
∴∠BAE=∠CGE,∠ABE=∠GCE,
∵BE=CE,
∴△ABE≌△GCE,
∴AB=CG,
又∵∠BAE=∠EAF,
∴∠CGE=∠EAF,
∴AF=GF,
∴AB=CG=GF+CF=AF+CF;
应用:如图,分别延长FB、GE,交于点H,
∵∠A=∠EBH=90°,∠GEA=∠HEB,AE=BE,
∴△AEG≌△BEH,
∴AG=BH,GE=HE,
又∵∠GEF=90°,即FE⊥GH,
∴FG=FH,
∵FH=BF+BH=BF+AG=![]() ,
,
∴GF=![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
解方程![]() ,这是一个一元四次方程,根据该方程的特点,它的解法通常是:设
,这是一个一元四次方程,根据该方程的特点,它的解法通常是:设![]() ,那么
,那么![]() ,于是原方程可变为
,于是原方程可变为![]() ①,解得
①,解得![]() ,
,![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]()
当![]() 时,
时,![]() ,∴
,∴![]()
∴原方程有四个根:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)在由原方程得到方程①的过程中,利用________法达到________的目的,体现了数学的转化思想.
(2)解方程![]() .
.
(3)已知非零实数a,b满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面直角坐标系中,二次函数y=ax2+bx+c与二次函数y=(a+3)x2+(b-15)x+c+18的图象与x轴的交点分别是A,B,C.
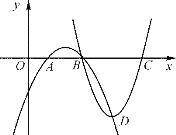
(1)判断图中经过点B,D,C的图象是哪一个二次函数的图象?试说明理由.
(2)设两个函数的图象都经过点B、D,求点B,D的横坐标.
(3)若点D是过点B、D、C的函数图象的顶点,纵坐标为-2,求这两个函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
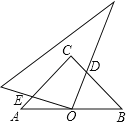
【题目】如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点0旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
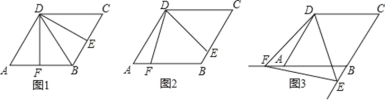
【题目】如图,四边形 ABCD 是边长为 2,一个锐角等于 60°的菱形纸片,将一个∠EDF=60°的三角形纸片的一个顶点与该菱形顶点 D 重合,按顺时针方向旋转这个三角形纸片,使它的两边分别交 CB,BA(或它们的延长线)于点 E, F;
①当 CE=AF 时,如图①,DE 与 DF 的数量关系是 ;
②继续旋转三角形纸片,当 CE≠AF 时,如图②,(1)的结论是否成立?若成立,加以证明;若不成立,请说明理由;
③再次旋转三角形纸片,当点 E,F 分别在 CB,BA 的延长线上时,如图③, 请直接写出 DE 与 DF 的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 顶点为
顶点为![]() ,且该抛物线与
,且该抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧).我们规定:抛物线与
的左侧).我们规定:抛物线与![]() 轴围成的封闭区域称为“
轴围成的封闭区域称为“![]() 区域”(不包含边界);横、纵坐标都是整数的点称为整点.
区域”(不包含边界);横、纵坐标都是整数的点称为整点.
(1)求抛物线![]() 顶点
顶点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)如果抛物线![]() 经过
经过![]() .
.
①求![]() 的值;
的值;
②在①的条件下,直接写出“![]() 区域”内整点的个数.
区域”内整点的个数.
(3)如果抛物线![]() 在“
在“![]() 区域”内有4个整点,直接写出
区域”内有4个整点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
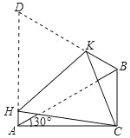
【题目】如图,在△ABC 中∠ACB=90°、∠CAB=30°,△ABD 是等边三角形将四边形 ACBD 折叠,使点 D 与点 C 重合,HK 为折痕,则cos∠ACH 的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com