
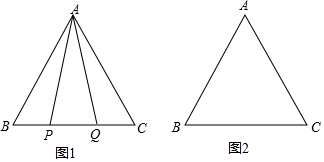
分析 (1)根据等腰三角形的性质得到∠APQ=∠AQP,由等边三角形得到∠B=60°,根据三角形外角的性质即可得到结论;
(2)由轴对称性质得,MP被AB垂直平分,从而得出AM=AP,∠BAP=∠BAM,再根据等量代换得出AM=AQ,然后根据AP=AQ,∠ABC=∠ACB=60°,得出∠QAM=∠CAB=60°,进而得出△MAQ是等边三角形,根据等边三角形的性质即可得到结论.
解答 解:(1)如图1,∵AP=AQ,
∴∠APQ=∠AQP,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠BAP=20°,
∴∠AQB=∠APQ=∠BAP+∠B=80°;
(2)①如图2所示: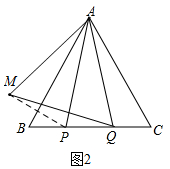
②(b)正确.
证明:如图2,由轴对称性质得,MP被AB垂直平分,
∴AM=AP,∠BAP=∠BAM,
又∵AP=AQ,
∴AM=AQ,
∵AP=AQ,
∴∠APQ=∠AQP,
又∵∠ABC=∠ACB=60°,
∴∠BAP=∠CAQ,
∴∠BAM=∠CAQ,
∴∠QAM=∠CAB=60°,
∴△MAQ是等边三角形,
∴QA=QM,即猜想(b)正确.
故答案为:(b)
点评 本题属于三角形综合题,主要考查了等边三角形的性质和判定,等腰三角形的性质,三角形的外角的性质,轴对称的性质的综合应用,熟练掌握等边三角形的判定和性质是解题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
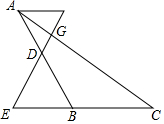 如图,在△ABC中,D是AB的中点,点E在CB的延长线上,AF∥BC,交ED的延长线于点F,EF交AC于点G,若CG:GA=3:1,BC=8,求AF的长.
如图,在△ABC中,D是AB的中点,点E在CB的延长线上,AF∥BC,交ED的延长线于点F,EF交AC于点G,若CG:GA=3:1,BC=8,求AF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
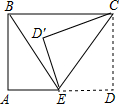 如图,四边形ABCD,AD∥BC,∠A=∠D=90°,E为AD中点,将点D绕着CE翻折到点D’处,连接BE,记∠AED’=α,∠ABE=β,则α与β之间的数量关系为( )
如图,四边形ABCD,AD∥BC,∠A=∠D=90°,E为AD中点,将点D绕着CE翻折到点D’处,连接BE,记∠AED’=α,∠ABE=β,则α与β之间的数量关系为( )| A. | α=β | B. | α=2β | C. | α+β=90° | D. | α+2β=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com