
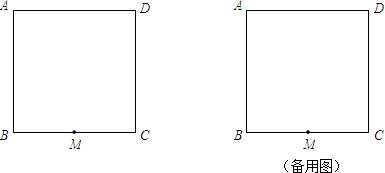
 解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,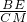 =
= ,
, BC=
BC= ×4=2,BE=e,CF=y,
×4=2,BE=e,CF=y,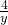 =
= ,EF=x+y=3+
,EF=x+y=3+ =
= ,
, (3+4-
(3+4- )×4-
)×4- ×4×1=
×4×1= EF×AN,
EF×AN, ;
; ①当F在CD的延长线上时,如图,
①当F在CD的延长线上时,如图, ,EF=x+y=
,EF=x+y=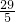 ,
, ×4×1-
×4×1- ×(
×( +5)×4=
+5)×4= EF×AN,
EF×AN, .
.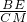 =
= ,代入求出xy=4即可;
,代入求出xy=4即可; ,EF=x+y═
,EF=x+y═ ,过A作AN⊥EF于N,根据面积公式求出即可;
,过A作AN⊥EF于N,根据面积公式求出即可; ,EF=x+y=
,EF=x+y=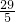 ,过A作AN⊥EF于N,根据面积公式求出即可.
,过A作AN⊥EF于N,根据面积公式求出即可.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
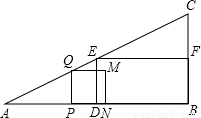
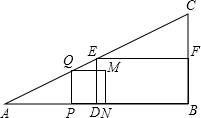 作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:
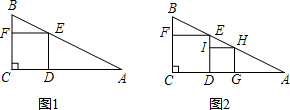 我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.| 4 |
| 3 |
| 4 |
| 3 |
| 2n |
| 3n-1 |
| 2n |
| 3n-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《四边形》(02)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com