

���� ��1�����������ε����ʺ͡������ı���ABCD���Ķ���������ͼ�Σ��ó�����C1�����ꣻ
��������ó���C��C1�����꣬����y��kx+b���ó������飬�ⷽ���鼴�ɣ�
��2��������������ٵ�AB=2BCʱ���ɵ�A������ó���C������Ϊ$��n\;��\;\frac{n-2}{2}��$��$��{n\;��\;\frac{2-n}{2}}��$����������ó����̣��ⷽ�̼��ɣ�
�ڵ�BC=2ABʱ��������ó���C������Ϊ��n��2n-4����n��4-2n������������ó����̣��ⷽ�̼��ɣ�
��� �⣺��1������ͼ1��ʾ����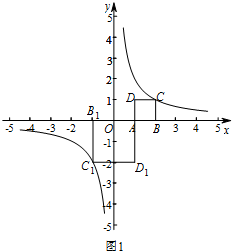 C1������Ϊ��-1��-2����
C1��������-1��-2����
�ʴ�Ϊ����-1��-2����
��������ã�C������Ϊ��n��n-m����C1������Ϊ��m-n��-n����
����y��kx+b�ã�$\left\{\begin{array}{l}{nk+b=n-m}\\{��m-n��k+b=-n}\end{array}\right.$��
��ã�k=1��b=-m��
�ʴ�Ϊ��1��-m��
��2��������������ٵ�AB=2BCʱ��
�ߵ�A������Ϊ��2��0����
���C������Ϊ$��n\;��\;\frac{n-2}{2}��$��$��{n\;��\;\frac{2-n}{2}}��$��
��$n��\frac{n-2}{2}=2$��$n��\frac{2-n}{2}=2$��
��ã�$n=1��\sqrt{5}$����ʵ����
���C������Ϊ$��{1+\sqrt{5}\;��\frac{{\sqrt{5}-1}}{2}}��$��$��{1-\sqrt{5}\;��\;\frac{{-\sqrt{5}-1}}{2}}��$��
�ڵ�BC=2ABʱ��
��C��������n��2n-4����n��4-2n����
��n��2n-4��=2��n��4-2n��=2��
��ã�$n=1��\sqrt{2}$��n=1��
���C������Ϊ$��{1+\sqrt{2}\;��\;2\sqrt{2}-2}��$��$��{1-\sqrt{2}\;��\;-2-2\sqrt{2}}��$��1��2����
������������C������Ϊ$��{1+\sqrt{5}\;��\frac{{\sqrt{5}-1}}{2}}��$��$��{1-\sqrt{5}\;��\;\frac{{-\sqrt{5}-1}}{2}}��$��$��{1+\sqrt{2}\;��\;2\sqrt{2}-2}��$��$��{1-\sqrt{2}\;��\;-2-2\sqrt{2}}��$��1��2����
���� �����Ƿ����������ۺ���Ŀ�������ˡ������ı���ABCD�������ʡ���������������ʽ�����á�һ�κ�������ʽ���������ε����ʣ����ε����ʡ����̵Ľⷨ��֪ʶ�������ۺ���ǿ����һ���Ѷȣ����⡰�����ı���ABCD���ǽ������Ĺؼ���


 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
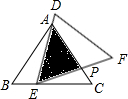 ��ͼ���ڡ�ABC�У���֪AB=AC=6��BC=8���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶�����DEʼ�վ�����A��EF��AC����P�㣮
��ͼ���ڡ�ABC�У���֪AB=AC=6��BC=8���ҡ�ABC�ա�DEF������DEF���ABC�غ���һ�𣬡�ABC��������DEF�˶��������㣺��E�ڱ�BC����B��C�ķ����˶�����DEʼ�վ�����A��EF��AC����P�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
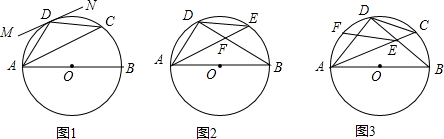
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2+a}{{-4-4a-{a^2}}}$ | B�� | $\frac{a-b}{b-a}$ | C�� | $\frac{{{x^2}-4}}{x-2}$ | D�� | $\frac{{{x^2}+{y^2}}}{x+y}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
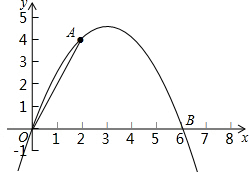 ��ͼ�����κ���y=ax2+bx��ͼ����A��2��4����B��6��0����
��ͼ�����κ���y=ax2+bx��ͼ����A��2��4����B��6��0�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com