
 ֱ��CB��y=3x+b�ֱ���x��y�ύ��C��-2��0����B���㣬����B��ֱ�߽�x���������ڵ�A����OB=OA��
ֱ��CB��y=3x+b�ֱ���x��y�ύ��C��-2��0����B���㣬����B��ֱ�߽�x���������ڵ�A����OB=OA������ ��1����ֱ��CB��y=3x+b�ֱ���x������C��-2��0�������b��ֵ�������ô���ϵ�������ֱ�ߵĽ���ʽ��
��2������S��BED=S��BDE���������εĸ���ȣ��õ�DE=DF����y=kx-k��k��0����x���ڵ�D���õ�D������꣬���õ�������з�����⣻
��3������BM=CM���ٸ��ݹ��ɶ����з�����⣻
�����ڡ�MONΪֱ�������Σ����Ե�M��N���п�����ֱ�Ƕ��㣬����OMN=90��ʱ��MN��x�ᣬ�õ�$\frac{AN}{AO}$=$\frac{AN}{AB}$���з�����⣬����NOM=90��ʱ����N��B�غϣ�AN=$\frac{3\sqrt{2}}{4}$t=6$\sqrt{2}$t���õ�t=8������ONM=90��ʱ����M��A�غϣ�t=8��AN=6$\sqrt{2}$����OM=6��AN���������������������
��� �⣺��1����ֱ��CBy=3x+b��x����C��-2��0����
��0=3��-2��+b��
��b=6��
��OB=OA����A��x���ϣ�
��A��6��0����
��ֱ��AB�Ľ���ʽ��y=-x+6��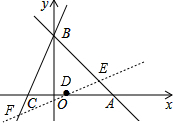
��2������
��ͼ��S��BED=S��BDE��
��DE=DF��
��$\left\{\begin{array}{l}{y=-x+6}\\{y=kx-k}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{k+6}{k+1}}\\{y=\frac{5k}{k+1}}\end{array}\right.$��
��E��$\frac{k+6}{K+1}$��$\frac{5k}{k+1}$����
��$\left\{\begin{array}{l}{y=3x+6}\\{y=kx-k}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{k+6}{k-3}}\\{y=\frac{9k}{k-3}}\end{array}\right.$��
��F��$\frac{k+6}{k-3}$��$\frac{9k}{k-3}$����
��ֱ��y=kx-k��x���ڵ�D��
��D��1��0����
��$\frac{k+6}{k+1}$-1=1-$\frac{k+6}{k-3}$��
��k=$\frac{3}{7}$��
��3���ٶ���M�ӵ�C������x�����A�˶����˶����ٶ�Ϊÿ��1����λ���ȣ���M�˶�t s��
��CM=t��OM=t-2��OB=6��
��BM=CM��
�ࣨt-2��2+62=t2��
��t=10��
�ڵ���OMN=90��ʱ��MN��x�ᣬ
��$\frac{AN}{AO}$=$\frac{AN}{AB}$��
��AM=8-t��
��AN=$\frac{3\sqrt{2}t}{4}$��
��$\frac{8-t}{6}$=$\frac{\frac{3\sqrt{2}}{4}}{6\sqrt{2}}$��
��t=$\frac{32}{7}$��
����NOM=90��ʱ����N��B�غϣ�AN=$\frac{3\sqrt{2}}{4}$t=6$\sqrt{2}$t��
��t=8��
����ONM=90��ʱ����M��A�غϣ�t=8��
AN=6$\sqrt{2}$��
��OM=6��AN��
�������
������������t=$\frac{32}{7}$��t=8ʱ����MONΪֱ�������Σ�
���� ������Ҫ��������ƽ��ֱ������ϵ���������꣬����ϵ������һ�κ����Ľ���ʽ���ⷽ�����֪ʶ����ۺ�Ӧ�ã�Ҫע����ǣ�3���У�Ҫ����ֱ��������ֱ�Ƕ���IJ�ͬλ�ý��з�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC��AB=AC��DE��ֱƽ��AB���ֱ�AB��AC��D��E���㣬��AB=12cm��BC=8cm����A=48�㣬���BCE���ܳ��͡�EBC�Ķ�����
��ͼ����֪��ABC��AB=AC��DE��ֱƽ��AB���ֱ�AB��AC��D��E���㣬��AB=12cm��BC=8cm����A=48�㣬���BCE���ܳ��͡�EBC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����O�ǡ�ABC�����Բ����֪��B=70�㣬���CAO�Ķ����ǣ�������
��ͼ��ʾ����O�ǡ�ABC�����Բ����֪��B=70�㣬���CAO�Ķ����ǣ�������| A�� | 20�� | B�� | 30�� | C�� | 35�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\sqrt{3}$ | C�� | -1 | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪a��b��С�ϰ����ǰ��ֱ�Ƕ������ֱ��b�ϣ�����1=38�㣬���2�Ķ���52�㣮
��ͼ����֪a��b��С�ϰ����ǰ��ֱ�Ƕ������ֱ��b�ϣ�����1=38�㣬���2�Ķ���52�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y1=a��x+2��2-3��y2=$\frac{1}{2}$��x-3��2+1���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�������½��ۣ�
��ͼ��������y1=a��x+2��2-3��y2=$\frac{1}{2}$��x-3��2+1���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�������½��ۣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com