
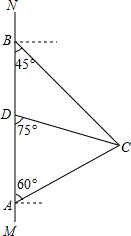
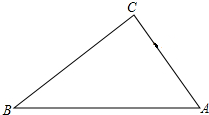
 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距$50(\sqrt{3}+1)$海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.分析 (1)作CE⊥AB,设AE=x海里,则BE=CE=$\sqrt{3}$x海里.根据AB=AE+BE=x+$\sqrt{3}$x=50($\sqrt{3}$+1),求得x的值后即可求得AC的长;
(2)作DF⊥AC于点F,根据AD的长和∠DAF的度数求线段DF的长后与50比较即可得到答案.
解答 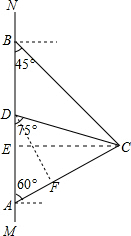 解:(1)如图,作CE⊥AB,
解:(1)如图,作CE⊥AB,
由题意得:∠ABC=45°,∠BAC=60°,
设AE=x海里,
在Rt△AEC中,CE=AE•tan60°=$\sqrt{3}$x;
在Rt△BCE中,BE=CE=$\sqrt{3}$x.
∴AE+BE=x+$\sqrt{3}$x=50($\sqrt{3}$+1),
解得:x=50.
AC=2x=100.
答:出A与C之间的距离是100海里;
(2)过点D作DF⊥AC于点F,
则DF=CF=$\sqrt{3}$AF=$\sqrt{3}$×50($\sqrt{3}$-1)≈63.2海里,
∵63.2>50,
所以巡逻船A沿直线AC航线,在去营救的途中没有触暗礁危险.
点评 本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
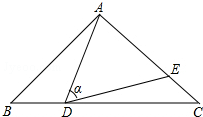 如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),
如图,在△ABC中,AB=AC=5,点D是边BC上一动点(不与B,C重合),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求:
已知:二次函数y=x2+bx+c的图象经过点A(0,-2)和点B(1,1),顶点为P.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→B→A直线运动,且速度为每秒2cm,设出发的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com