
【题目】如图,点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA,给出以下结论:①DE平分∠BDC; ②△BCE是等边三角形;③∠AEB=45°;④DE=AD+CD;正确的结论有_____.(请填序号)
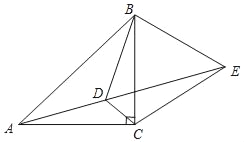
【答案】①②③④.
【解析】
①先根据等腰直角三角形的性质及已知条件得出∠DAB=∠DBA=30°,则AD=BD,再证明CD是边AB的垂直平分线,得出∠ACD=∠BCD=45°,然后根据三角形外角的性质求出∠CDE=∠BDE=60°即可;
②先利用等角对等边证BC=CE,再推得∠BCE=60°可得结论;
③利用差可求得结论:∠AEB=∠BEC-∠AEC;
④截取DG=DC,证明△DCG是等边三角形,再证明△ACD≌△ECG,利用线段的和与等量代换可得结论.
解:①∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°-15°=30°,
∴BD=AD,
∴D在AB的垂直平分线上,
∵AC=BC,
∴C也在AB的垂直平分线上,
即直线CD是AB的垂直平分线,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠CAD+∠ACD=15°+45°=60°,
∵∠BDE=∠DBA+∠BAD=60°;
∴∠CDE=∠BDE,
即DE平分∠BDC;
所以①正确;
②∵CA=CB,CA=CE,
∴CB=CE,
∵∠CAD=∠AEC=15°,
∴∠ACE=180°-15°-15°=150°,
∵∠ACB=90°,
∴∠BCE=150°-90°=60°,
∴△BCE是等边三角形;
所以②正确;
③∵△BCE是等边三角形,
∴∠BEC=60°,
∵∠AEC=15°,
∴∠AEB=60°-15°=45°,
所以③正确;
④在DE上取一点G,使DC=DG,连接CG,
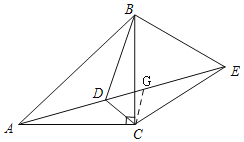
∵∠EDC=60°,
∴△DCG是等边三角形,
∴DC=DG=CG,∠DCG=60°,
∴∠GCE=150°-60°-45°=45°,
∴∠ACD=∠GCE=45°,
∵AC=CE,
∴△ACD≌△ECG,
∴EG=AD,
∴DE=EG+DG=AD+DC,
所以④正确;
正确的结论有:①②③④;
故答案为::①②③④.


科目:初中数学 来源: 题型:
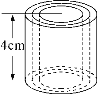
【题目】如图,圆柱的高是4cm,当圆柱底面半径r(cm)变化时,圆柱的体积V(cm3)也随之变化.
(1)在这个变化过程中,写出自变量,因变量;
(2) 写出圆柱的体积V与底面半径r的关系式;
(3)当圆柱的底面半径由2cm变化到8cm时,圆柱的体积由多少cm3变化到多少cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
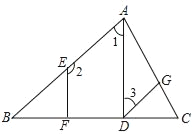
【题目】如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株? 小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3﹣0.5x)元,
由题意得(x+3)(3﹣0.5x)=10,
化简,整理得:x2﹣3x+2=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系: .
(2)请用一种与小明不相同的方法求解上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF=![]() S△ABC.其中正确的个数有( )
S△ABC.其中正确的个数有( )
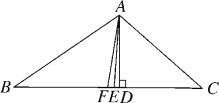
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是两棵大树,两棵大树之间有一个废弃的圆形坑塘,为开发利用这个坑塘,需要测量A,B之间的距离,但坑塘附近地形复杂不容易直接测量.
(1)请你利用所学知识,设计一个测量A,B之间的距离的方案,并说明理由;
(2)在你设计的测量方案中,需要测量哪些数据?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题: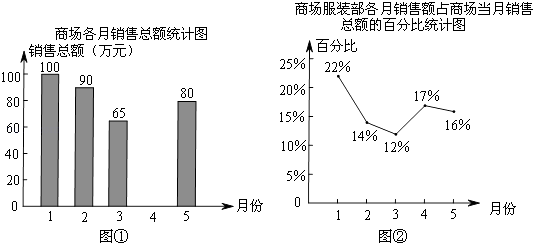
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,那么改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)如表1所示,如果经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负整数,请写出每次“操作”后所得的数表;(写出一种方法即可)
1 | 2 | 3 | -7 |
-2 | -1 | 0 | 1 |
表1
(2)如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a的值.
a | a2-1 | -a | -a2 |
2-a | 1-a2 | a-2 | a2 |
表2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.注意:添加四个符合要求的正方形,并用阴影表示.
(2)先用三角板画∠AOB=60°,∠BOC=45°,然后计算∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com