Question

9．（1）如图（1）AB∥CD，若BF、DF分别平分∠ABE、∠CDE，试探求∠E与∠F的关系；
（2）如图（2）AB∥CD，若BF、DF分别是∠ABE、∠CDE的三等分线（∠ABF=$\frac{1}{3}$∠ABE，∠CDF=$\frac{1}{3}$∠CDE），∠E与∠F有何关系，并说明理由．

Answer 1

分析 （1）首先连接FE并延长，易得∠BED=∠BFD+∠EBF+∠EDF，又由BF、DF分别平分∠ABE、∠CDE，以及（1）的结论，易证得∠BED=2∠BFD；
（2）过点E、F分别作AB的平行线EG、FH，由平行线的传递性可得AB∥EG∥FH∥CD，根据平行线的性质得到∠ABF=∠BFH，∠CDF=∠DFH，根据已知条件即可得到结论．

解答 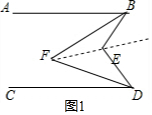解：（1）∠BED=2∠BFD．
证明：连接FE并延长，
∵∠BEG=∠BFE+∠EBF，∠DEG=∠DFE+∠EDF，
∴∠BED=∠BFD+∠EBF+∠EDF，
∵BF、DF分别平分∠ABE、∠CDE，
∴∠ABE+∠CDE=2（∠EBF+∠EDF），
∵∠BED=∠ABE+∠CDE，
∴∠EBF+∠EDF=$\frac{1}{2}$∠BED，
∴∠BED=∠BFD+$\frac{1}{2}$∠BED，
∴∠BED=2∠BFD；
（2）过点E、F分别作AB的平行线EG、FH，由平行线的传递性可得AB∥EG∥FH∥CD，
∵AB∥FH，
∴∠ABF=∠BFH，
∵FH∥CD，
∴∠CDF=∠DFH，
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF；
同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE；
∵∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=$\frac{1}{3}$（∠ABE+∠CDE）=$\frac{1}{3}$∠BED，
∴∠BED=3∠BFD．

点评 此题考查了平行线的性质以及角平分线的定义．此题难度较大，注意掌握数形结合思想与整体思想的应用．