
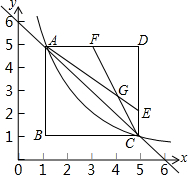
 如图,若直线y=-x+6与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m)与C(n,1)两点,以线段AC为斜边,在AC的两侧作等腰直角三角形ABC和ADC,其中∠B=∠D=90°,F为AD的中点,点E在边CD上,且DE=3EC,AE与CF相交于点G.
如图,若直线y=-x+6与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m)与C(n,1)两点,以线段AC为斜边,在AC的两侧作等腰直角三角形ABC和ADC,其中∠B=∠D=90°,F为AD的中点,点E在边CD上,且DE=3EC,AE与CF相交于点G.分析 (1)求出A(1,5),得出k=5即可;
(2)由等腰直角三角形的性质得出AB=BC=AD=CD,即可得出四边形ABCD是正方形;
(3)取BC的中点M,连接AM、EM,证明△CEM∽△DFC,得出∠CME=∠DCF,同理:△CEM∽△BMA,得出$\frac{EM}{MA}=\frac{CM}{AB}$=$\frac{CE}{BM}$=$\frac{1}{2}$,∠CME=∠BAM,再证出△CEM∽△MEA,得出∠CME=∠MAE,证出∠MAE=∠DCF,证明四边形AMCF是平行四边形,由平行线的性质得出∠AGF=∠MAE,即可得出结论;
(4)求出直线AE的解析式为y=-$\frac{3}{4}$x+$\frac{23}{4}$,同理:直线CF的解析式为y=-2x+11,解方程组$\left\{\begin{array}{l}{y=-\frac{3}{4}x+\frac{23}{4}}\\{y=-2x+11}\end{array}\right.$得出G($\frac{21}{5}$,$\frac{13}{5}$),过G作GM∥AD,交双曲线y=$\frac{5}{x}$于M,则M的纵坐标为$\frac{13}{5}$,由反比例函数解析式求出求出M的横坐标即可.
解答 (1)解:∵直线y=-x+6与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m)与C(n,1)两点,
∴m=-1+6=5,-n+6=1,
∴m=n=5,
∴A(1,5),
代入y=$\frac{k}{x}$得:k=1×5=5;
(2)解:四边形ABCD是正方形,理由如下:
∵以线段AC为斜边,在AC的两侧作等腰直角三角形ABC和ADC,∠B=∠D=90°,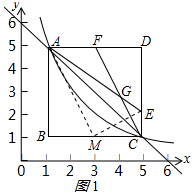
∴B(1,1),AB=BC=AD=CD,
∴四边形ABCD是正方形;
(3)证明:取BC的中点M,连接AM、EM,如图1所示:
∵四边形ABCD是正方形,A(1,5),
∴AD∥BC,AB=BC=CD=AD=4,∠B=∠MCE=∠CDF=90°,
∵DE=3EC,
∴CE=1,BM=CM=2,
∵F为AD的中点,
∴AF=DF=2,
∴$\frac{CE}{DF}=\frac{CM}{CD}$=$\frac{1}{2}$,
∴△CEM∽△DFC,
∴∠CME=∠DCF,
同理:△CEM∽△BMA,
∴$\frac{EM}{MA}=\frac{CM}{AB}$=$\frac{CE}{BM}$=$\frac{1}{2}$,∠CME=∠BAM,
∵∠BAM+∠BMA=90°,
∴∠CME+∠BMA=90°,
∴∠AME=90°,
∵$\frac{EM}{MA}=\frac{CE}{CM}$=$\frac{1}{2}$,
∴△CEM∽△MEA,
∴∠CME=∠MAE,
∴∠MAE=∠DCF,
∵AF∥CM,AF=CM=2,
∴四边形AMCF是平行四边形,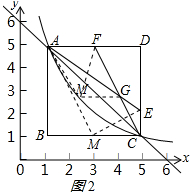
∴AM∥CF,
∴∠AGF=∠MAE,
∴∠AGF=∠DCF;
(4)解:设直线AE的解析式为y=kx+b,
∵A(1,5),E(5,2),
∴$\left\{\begin{array}{l}{k+b=5}\\{5k+b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{23}{4}}\end{array}\right.$,
∴直线AE的解析式为y=-$\frac{3}{4}$x+$\frac{23}{4}$,
同理:直线CF的解析式为y=-2x+11,
解方程组$\left\{\begin{array}{l}{y=-\frac{3}{4}x+\frac{23}{4}}\\{y=-2x+11}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{21}{5}}\\{y=\frac{13}{5}}\end{array}\right.$,
∴G($\frac{21}{5}$,$\frac{13}{5}$),
过G作GM∥AD,交双曲线y=$\frac{5}{x}$于M,如图2所示:
则M的纵坐标为$\frac{13}{5}$,△AFM的面积=△AFG的面积,
∴M的横坐标=5÷$\frac{13}{5}$=$\frac{25}{13}$,
∴M($\frac{25}{13}$,$\frac{13}{5}$).
点评 本题是反比例函数综合题目,考查了反比例函数解析式的求法、正方形的判定与性质、坐标与图形性质、相似三角形的判定与性质、待定系数法求一次函数的解析式等知识;本题综合性强,难度较大.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了审核书稿中的错别字,选择抽样调查 | |
| B. | 为了了解春节联欢晚会的收视率,选择全面调查 | |
| C. | “射击运动员射击一次,命中靶心”是随机事件 | |
| D. | “366人中至少有2人的生日是同月同日”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
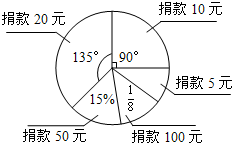 在抗震救灾的捐款活动中,六(2)班同学的捐款人数情况如图所示,其中捐款10元的人数为10人.请根据图象回答下列问题:
在抗震救灾的捐款活动中,六(2)班同学的捐款人数情况如图所示,其中捐款10元的人数为10人.请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com