
分析 首先把第一个分式分式的分子和分母分解因式,把括号内的式子通分相加,把除法转化为乘法,即可化简,然后求值即可.
解答 解:原式=$\frac{a(a-3b)}{(a+b)(a-b)}$÷$\frac{a-b+a+b}{(a+b)(a-b)}$
=$\frac{a(a-3b)}{(a+b)(a-b)}$÷$\frac{2a}{(a+b)(a-b)}$
=$\frac{a(a-3b)}{(a+b)(a-b)}$•$\frac{(a+b)(a-b)}{2a}$
=$\frac{a-3b}{2}$.
∵a-3b-4=0,
∴a-3b=4.
∴原式=$\frac{4}{2}$=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则正确对分式进行通分、约分是解本题的关键.


科目:初中数学 来源: 题型:解答题
 有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是70米.甲、乙两机器人分别从A、B两点同时同向出发,乙机器人始终以60米/分的速度行走,乙行走7分钟到达C点.设两机器人出发时间为t(分钟),当t=2分钟时,甲追上乙.前3分钟甲机器人的速度保持不变,3分钟后甲的速度变为另一数值.已知在3≤t≤4分钟时,甲、乙两机器人之间的距离保持不变.
有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是70米.甲、乙两机器人分别从A、B两点同时同向出发,乙机器人始终以60米/分的速度行走,乙行走7分钟到达C点.设两机器人出发时间为t(分钟),当t=2分钟时,甲追上乙.前3分钟甲机器人的速度保持不变,3分钟后甲的速度变为另一数值.已知在3≤t≤4分钟时,甲、乙两机器人之间的距离保持不变.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
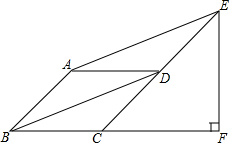 如图,在?ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F.
如图,在?ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
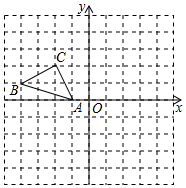 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:解答题
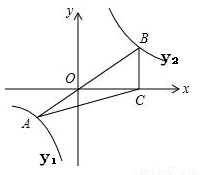
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数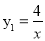 (x<0)图象上一点,AO的延长线交函数
(x<0)图象上一点,AO的延长线交函数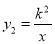 (x>0,k<0)的
(x>0,k<0)的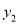 图象于点B,BC⊥x轴,若S△ABC=
图象于点B,BC⊥x轴,若S△ABC=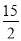 ,求函数y2的解析式.
,求函数y2的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com