
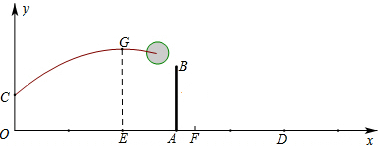
分析 (1)根据此时抛物线顶点坐标为(7,3.2),设解析式为y=a(x-7)2+3.2,再将点C坐标代入即可求得;
(2)由(1)中解析式求得x=9.5时y的值,与他起跳后的最大高度为3.1米比较即可得;
(3)设抛物线解析式为y=a(x-7)2+h,将点C坐标代入得到用h表示a的式子,再根据球既要过球网,又不出边界即x=9时,y>2.43且x=18时,y≤0得出关于h的不等式组,解之即可得.
解答 解:(1)根据题意知此时抛物线的顶点G的坐标为(7,3.2),
设抛物线解析式为y=a(x-7)2+3.2,
将点C(0,1.8)代入,得:49a+3.2=1.8,
解得:a=-$\frac{1}{35}$,
∴排球飞行的高度y与水平距离x的函数关系式为y=-$\frac{1}{35}$(x-7)2+$\frac{16}{5}$;
(2)由题意当x=9.5时,y=-$\frac{1}{35}$(9.5-7)2+$\frac{16}{5}$≈3.02<3.1,
故这次她可以拦网成功;
(3)设抛物线解析式为y=a(x-7)2+h,
将点C(0,1.8)代入,得:49a+h=1.8,即a=$\frac{1.8-h}{49}$,
∴此时抛物线解析式为y=$\frac{1.8-h}{49}$(x-7)2+h,
根据题意,得:$\left\{\begin{array}{l}{\frac{4(1.8-h)}{49}+h>2.43}\\{\frac{121(1.8-h)}{49}+h≤0}\end{array}\right.$,
解得:h≥3.025,
答:排球飞行的最大高度h的取值范围是h≥3.025.
点评 此题主要考查了二次函数的应用题,求范围的问题,可以利用临界点法求出自变量的值,再根据题意确定范围.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
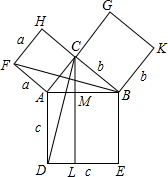 △ABC是以∠ACB为直角的直角三角形,以AB、BC、AC为边作正方形ABED、BCGK、ACHF,过点C作CL⊥DE交AB于点M,交DE于点L,连接CD、BF.求证:a2+b2=c2.
△ABC是以∠ACB为直角的直角三角形,以AB、BC、AC为边作正方形ABED、BCGK、ACHF,过点C作CL⊥DE交AB于点M,交DE于点L,连接CD、BF.求证:a2+b2=c2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-a)2(x-a+1) | B. | (x-a)2(x-a-1) | C. | (x-a)2(x+a) | D. | (a-x)2(x-a-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48 cm | B. | 54 cm | C. | 56 cm | D. | 64 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,AB=AC=20厘米,BC=16厘米,点D为AB的中点.如果点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①设点P运动的时间为t,用含有t的代数式表示线段PC的长度;②若点Q的运动速度与点P的运动速度相等,经过t秒后,△BPD与△CQP是否全等,求t的值.
如图,已知△ABC中,AB=AC=20厘米,BC=16厘米,点D为AB的中点.如果点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①设点P运动的时间为t,用含有t的代数式表示线段PC的长度;②若点Q的运动速度与点P的运动速度相等,经过t秒后,△BPD与△CQP是否全等,求t的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com