
 (2012•重庆)企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:
(2012•重庆)企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| 输送的污水量y1(吨) | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 12 |
| 231 |
| 419 |
| 809 |
| k |
| x |
| 12000 |
| x |
|
|
| 12000 |
| x |
| 1 |
| 2 |
| 12000 |
| x |
| 3 |
| 4 |
| 1 |
| 12 |
| b |
| 2a |
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| 2a |
-17±
| ||
| 20 |
| 809 |


科目:初中数学 来源: 题型:阅读理解
 2012年3月23日至3月25日为期3天、以“云联世界感知未来”为主题的2012中国(重庆)国际云计算博览会(下称云博会)在渝召开,重庆新市委书记张德江说在未来10年内重庆实施“云端计划”建设智慧重庆. 市委市政府非常重视“云端服务器”的建设,几年前就已经着手建设“云端服务器”,据统计,某行政区在去年前7个月内,“云端服务器”的数量与月份之间的关系如下表:
2012年3月23日至3月25日为期3天、以“云联世界感知未来”为主题的2012中国(重庆)国际云计算博览会(下称云博会)在渝召开,重庆新市委书记张德江说在未来10年内重庆实施“云端计划”建设智慧重庆. 市委市政府非常重视“云端服务器”的建设,几年前就已经着手建设“云端服务器”,据统计,某行政区在去年前7个月内,“云端服务器”的数量与月份之间的关系如下表:| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 云端服务器数量y1(台) | 32 | 34 | 36 | 38 | 40 | 42 | 44 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2012年3月23日至3月25日为期3天、以“云联世界感知未来”为主题的2012中国(重庆)国际云计算博览会(下称云博会)在渝召开,重庆新市委书记张德江说在未来10年内重庆实施“云端计划”建设智慧重庆. 市委市政府非常重视“云端服务器”的建设,几年前就已经着手建设“云端服务器”,据统计,某行政区在去年前7个月内,“云端服务器”的数量与月份之间的关系如下表:
2012年3月23日至3月25日为期3天、以“云联世界感知未来”为主题的2012中国(重庆)国际云计算博览会(下称云博会)在渝召开,重庆新市委书记张德江说在未来10年内重庆实施“云端计划”建设智慧重庆. 市委市政府非常重视“云端服务器”的建设,几年前就已经着手建设“云端服务器”,据统计,某行政区在去年前7个月内,“云端服务器”的数量与月份之间的关系如下表:| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 云端服务器数量y1(台) | 32 | 34 | 36 | 38 | 40 | 42 | 44 |
查看答案和解析>>
科目:初中数学 来源:2012届重庆巴蜀中学九年级中考第五次6月考试押题数学试卷(带解析) 题型:解答题
2012年3月23日至3月25日为期3天、以“云联世界感知未来”为主题的2012中国(重庆)国际云计算博览会(下称云博会)在渝召开,重庆新市委书记张德江说在未来10年内重庆实施“云端计划” 建设智慧重庆。 市委市政府非常重视“云端服务器”的建设,几年前就已经着手建设“云端服务器”,据统计,某行政区在去年前7个月内,“云端服务器”的数量与月份之间的关系如下表:
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
云端服务器数量 (台) (台) | 32 | 34 | 36 | 38 | 40 | 42 | 44 |
 (台)与月份x(月)之间存在如图所示的变化趋势:
(台)与月份x(月)之间存在如图所示的变化趋势:
 与x之间的函数关系式,根据如图所示的变化趋势,直接写出
与x之间的函数关系式,根据如图所示的变化趋势,直接写出 与x之间满足的一次函数关系式;
与x之间满足的一次函数关系式; (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式:  ,(1≤x≤7,且x为整数);8至12月份的资金投入
,(1≤x≤7,且x为整数);8至12月份的资金投入 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式: (8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
(8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;查看答案和解析>>
科目:初中数学 来源:2012年重庆市巴蜀中学中考数学模拟试卷(6月份)(解析版) 题型:解答题
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 云端服务器数量y1(台) | 32 | 34 | 36 | 38 | 40 | 42 | 44 |

查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆巴蜀中学九年级中考第五次6月考试押题数学试卷(解析版) 题型:解答题
2012年3月23日至3月25日为期3天、以“云联世界感知未来”为主题的2012中国(重庆)国际云计算博览会(下称云博会)在渝召开,重庆新市委书记张德江说在未来10年内重庆实施“云端计划” 建设智慧重庆。 市委市政府非常重视“云端服务器”的建设,几年前就已经着手建设“云端服务器”,据统计,某行政区在去年前7个月内,“云端服务器”的数量与月份之间的关系如下表:
|
月份x(月) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
云端服务器数量 |
32 |
34 |
36 |
38 |
40 |
42 |
44 |
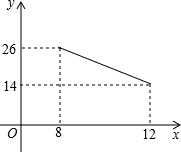
而由于部分地区陆续被划分到其它行政区,该行政区8至12月份“云端服务器”数量 (台)与月份x(月)之间存在如图所示的变化趋势:
(台)与月份x(月)之间存在如图所示的变化趋势:

(1)请观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出 与x之间的函数关系式,根据如图所示的变化趋势,直接写出
与x之间的函数关系式,根据如图所示的变化趋势,直接写出 与x之间满足的一次函数关系式;
与x之间满足的一次函数关系式;
(2)在2011年内,市政府每月对每一台云端服务器的资金也随月份发生改变,若对每一台服务器的投入的资金 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式:  ,(1≤x≤7,且x为整数);8至12月份的资金投入
,(1≤x≤7,且x为整数);8至12月份的资金投入 (万元)与月份x满足函数关系式:
(万元)与月份x满足函数关系式: (8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
(8≤x≤12,且x为整数)求去年哪个月政府对该片区的资金投入最大,并求出这个最大投入;
(3)2012年1月到3月份,政府计划该区的云端服务器每月的数量比去年12份减少2a%,在去年12月份的基础上每月每一台云端服务器资金投入量将增加0.5a%,某民营企业为表示对“智慧重庆”的鼎力支持,决定在1月到3月份对每台云端服务器分别赞助3万元。若计划1月到3月份用于云端服务器所需的资金总额(政府+民企赞助)一共达到546万元,请参考以下数据,估计a的整数值。(参考数据:172=289,182=324,192=361)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com