
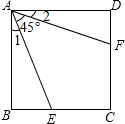
 如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:分析 先证明Rt△ABE≌Rt△ADF得到∠1=∠2,易得∠1=∠2=∠22.5°,于是可对①进行判断;连结EF、AC,它们相交于点H,如图,利用Rt△ABE≌Rt△ADF得到BE=DF,则CE=CF,接着判断AC垂直平分EF,AH平分∠EAF,于是利用角平分线的性质定理得到EB=EH,FD=FH,则可对③④进行判断;设BE=x,则EF=2x,CE=1-x,利用等腰直角三角形的性质得到2x=$\sqrt{2}$(1-x),解得x=$\sqrt{2}$-1,则可对④进行判断.
解答 解:∵四边形ABCD为正方形,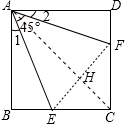
∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中
$\left\{\begin{array}{l}{AE=AF}\\{AB=AD}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF,
∴∠1=∠2,
∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正确;
连结EF、AC,它们相交于点H,如图,
∵Rt△ABE≌Rt△ADF,
∴BE=DF,
而BC=DC,
∴CE=CF,
而AE=AF,
∴AC垂直平分EF,AH平分∠EAF,
∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,所以④错误;
∴△ECF的周长=CE+CF+EF=CE+BE+CF+DF=CB+CD=1+1=2,所以③正确;
设BE=x,则EF=2x,CE=1-x,
∵△CEF为等腰直角三角形,
∴EF=$\sqrt{2}$CE,即2x=$\sqrt{2}$(1-x),解得x=$\sqrt{2}$-1,
∴EF=2($\sqrt{2}$-1),
∴CH=$\frac{1}{2}$EF=$\sqrt{2}$-1,所以②正确.
故答案为①②③.
点评 本题考查了四边形的综合题:熟练掌握正方形的性质和角平分线的性质定理.解决本题的关键是证明AC垂直平分EF.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
 假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )
假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
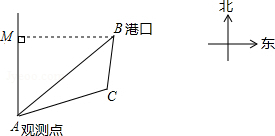 已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10$\sqrt{2}$km,一艘货轮从B港口沿如图所示的BC方向航行4$\sqrt{7}$km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10$\sqrt{2}$km,一艘货轮从B港口沿如图所示的BC方向航行4$\sqrt{7}$km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.| A. | 8$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 7$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个有理数的和是无理数 | |
| B. | 从装有5个红球和1个白球的袋子中随机摸出1球是白球 | |
| C. | 买一张电影票,座位号是偶数 | |
| D. | 购买1张彩票中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
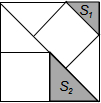 有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )| A. | 1:$\sqrt{2}$ | B. | 1:2 | C. | 2:3 | D. | 4:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
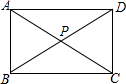 如图,已知四边形ABCD是矩形,对角线AC,BD交于点P,则下列结论正确的是( )
如图,已知四边形ABCD是矩形,对角线AC,BD交于点P,则下列结论正确的是( )| A. | AC是∠BAD的平分线 | B. | AC⊥BD | ||
| C. | AC=BD | D. | AC>2BP |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com