
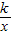 的图象上,那么下列各点中,不在反比例函数y=-
的图象上,那么下列各点中,不在反比例函数y=- 的图象上的点是( )
的图象上的点是( ) 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 1 | s |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、在一次抛掷硬币的试验中,甲同学说:“我只做了10次试验就得到了正面朝上的概率为30%”; | ||
| B、某同学在抛掷两枚硬币的试验中做了400次,得到“一正一反”的频率为26.7%,如果再做400次,得到的频率仍然是26.7%; | ||
C、在投掷一枚均匀的正方体骰子的试验中,小明得到“1点朝上”的概率为
| ||
| D、在抛掷一枚硬币的试验中,小刚为了节约时间,同时抛掷5枚硬币,这样得到的结果不会受到影响 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,平面直角坐标系上有A(a,0)、B(0,-b)、C(b,0)三点,且a≥b>0,抛物线y=(x-2)(x-m)-(n-2)(n-m). (m,n为常数,且m+2≥2n>0),经过点A和点C,顶点为P
已知,平面直角坐标系上有A(a,0)、B(0,-b)、C(b,0)三点,且a≥b>0,抛物线y=(x-2)(x-m)-(n-2)(n-m). (m,n为常数,且m+2≥2n>0),经过点A和点C,顶点为P查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.在一次抛掷硬币的试验中,甲同学说:“我只做了10次试验就得到了正面朝上的概率为30%”; | ||
| B.某同学在抛掷两枚硬币的试验中做了400次,得到“一正一反”的频率为26.7%,如果再做400次,得到的频率仍然是26.7%; | ||
C.在投掷一枚均匀的正方体骰子的试验中,小明得到“1点朝上”的概率为
| ||
| D.在抛掷一枚硬币的试验中,小刚为了节约时间,同时抛掷5枚硬币,这样得到的结果不会受到影响 |
查看答案和解析>>
科目:初中数学 来源:《6.1 频率与概率》2010年同步练习(解析版) 题型:选择题
 ,那么他再做300次试验,一定有50次“1点朝上”;
,那么他再做300次试验,一定有50次“1点朝上”;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com