
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| 乙 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
分析 根据方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]分别求出两种水稻的产量的方差,再进行比较即可.
解答 解:甲种水稻产量的方差是:$\frac{1}{5}$[(9.4-10)2+(10.3-10)2+(10.8-10)2+(9.7-10)2+(9.8-10)2]=0.244.
乙种水稻产量的方差是:$\frac{1}{5}$[(9.8-10)2+(9.9-10)2+(10.1-10)2+(10-10)2+(10.2-10)2]=0.02,
∴0.02<0.244,
∴产量比较稳定的水稻品种是乙.
故答案为:乙.
点评 此题考查了方差,用到的知识点是方差和平均数的计算公式,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
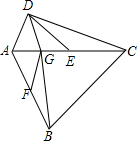 如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,
如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
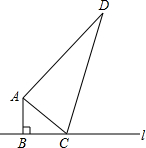 如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?
如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 阅读 | 专业 | 表达 | |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com