
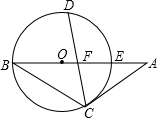
 如图,以△ABC的边AB上一点O为圆心的圆经过B、C两点,且与边AB相交于点E,D是弧BE的中点,CD交AB于F,AC=AF.
如图,以△ABC的边AB上一点O为圆心的圆经过B、C两点,且与边AB相交于点E,D是弧BE的中点,CD交AB于F,AC=AF.| 37 |
| 37 |
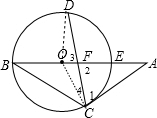 (1)证明:连结OD、OC,如图,
(1)证明:连结OD、OC,如图,| 37 |


科目:初中数学 来源: 题型:
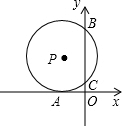 如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )
如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )| A、(-3,4) |
| B、(-4,6) |
| C、(-3,5) |
| D、(-4,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 25 |
| 3 | -8 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
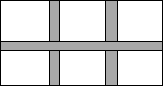 新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为
新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在万三中的“创造节”上,数学兴趣小组长小明想要知道旗杆的直径.苦于身边没有直尺和测量工具,只有一根已知长为30厘米的细线,他用这个细线刚好将旗杆缠了三圈,每缠一圈,细线上升6厘米,请你帮助小明算出旗杆的直径是
如图,在万三中的“创造节”上,数学兴趣小组长小明想要知道旗杆的直径.苦于身边没有直尺和测量工具,只有一根已知长为30厘米的细线,他用这个细线刚好将旗杆缠了三圈,每缠一圈,细线上升6厘米,请你帮助小明算出旗杆的直径是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com