
【题目】如图,已知同一平面内,∠AOB=90゜,∠AOC=60゜.
(1)填空:∠COB=;
(2)如OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为;
(3)试问在(2)的条件下,如果将题目中∠AOC=60゜改成∠AOC=2α(α<45゜),其他条件不变,你能求出∠DOE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
【答案】
(1)解:分为两种情况::①如图1,当射线OC在∠AOB内部时,∠COB=∠AOB﹣∠AOC=90°﹣60°=30°;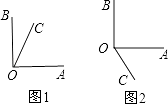 ②如图2,当射线OC在∠AOB外部时,∠COB=∠AOB+∠AOC=90°+60°=150°;故答案为:150°或30°
②如图2,当射线OC在∠AOB外部时,∠COB=∠AOB+∠AOC=90°+60°=150°;故答案为:150°或30°
(2)解:( 2 )在图3中,∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,∴∠DOC= ![]() ∠BOC=
∠BOC= ![]() ×30°=15°,∠COE=
×30°=15°,∠COE= ![]() ∠AOC=
∠AOC= ![]() ×60°=30°,
×60°=30°,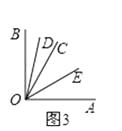
 ∴∠DOE=∠COD+∠COE=15°+30°=45°;在图4中,∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,∴∠DOC=
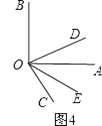
∴∠DOE=∠COD+∠COE=15°+30°=45°;在图4中,∵∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC,∴∠DOC= ![]() ∠BOC=
∠BOC= ![]() ×(90°+60°)=75°,∠COE=
×(90°+60°)=75°,∠COE= ![]() ∠AOC=
∠AOC= ![]() ×60°=30°,∴∠DOE=∠COD﹣∠COE=75°﹣30°=45°;故答案为:45°.
×60°=30°,∴∠DOE=∠COD﹣∠COE=75°﹣30°=45°;故答案为:45°.
(3)解:能求出∠DOE的度数.
①当OC在∠AOB内部时,如图3,

∵∠AOB=90°,∠AOC=2α°,
∴∠BOC=∠AOB﹣∠AOC=90°﹣2α°,
∵OD、OE分别平分∠BOC,∠AOC,
∴∠DOC= ![]() ∠BOC=45°﹣α°,∠COE=
∠BOC=45°﹣α°,∠COE= ![]() ∠AOC=α°,
∠AOC=α°,
∴∠DOE=∠DOC+∠COE=(45°﹣α°)+α°=45°;
②当OC在∠AOB外部时,如图4,

∵∠AOB=90,∠AOC=2α°,
∴∠BOC=∠AOB+∠AOC=90°+2α°,
∵OD、OE分别平分∠BOC,∠AOC,
∴∠DOC= ![]() ∠BOC=45°+α°,∠COE=
∠BOC=45°+α°,∠COE= ![]() ∠AOC=α°,
∠AOC=α°,
∴∠DOE=∠DOC﹣∠COE=(45°+α°)﹣α°=45°;
综合上述,∠DOE=45°
【解析】(1)根据题意分两种情况画出图形:当①如图1,当射线OC在∠AOB内部时,②如图2,当射线OC在∠AOB外部时,分别求出∠BOC的度数。
(2)根据题意分两种情况画出图形:根据已知条件OD平分∠BOC,OE平分∠AOC,分别求出∠DOC,∠COE的度数,然后根据∠DOE=∠COD+∠COE或∠DOE=∠COD﹣∠COE,即可求解。
(3)根据题意分两种情况画出图形:①当OC在∠AOB内部时,如图3,②当OC在∠AOB外部时,如图4,先根据角平分线的定义用含α°的代数式分别表示出∠DOC,∠COE的度数,再根据∠DOE=∠DOC+∠COE和∠DOE=∠DOC﹣∠COE,即可求出结果。


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C为数轴上的三点,动点A、B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点C对应的数为8.
(1)若2秒后,a、b满足|a+8|+(b﹣2)2=0,则x= , y= , 并请在数轴上标出A、B两点的位置.
(2)若动点A、B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得|a|=|b|,使得z= .
(3)若动点A、B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t= . ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com