
【题目】如图,已知![]() 为
为![]() 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.
(1)作![]() 的平分线
的平分线![]() .
.
(2)在![]() 上取一点
上取一点![]() ,使得
,使得![]() .
.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,这时他发现
,这时他发现![]() 与
与![]() 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

【答案】(1)答案见解析;(2)答案见解析;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)以点O为圆心,以任意长为半径画弧与∠AOB的两边分别相交,再以两交点为圆心,以大于两交点之间的距离的一半为半径画弧,相交于一点,过这一点与O作射线OC即可;
(2)在OC上取一点P,使得OP=a;
(3)以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,PN⊥OB于N,根据角平分线上的点到角的两边的距离相等可得PM=PN,利用HL证明△E2PM≌△DPN,得出∠OE2P=∠ODP,再根据平角的定义即可求解.
试题解析:(1)如图,OC即为所求;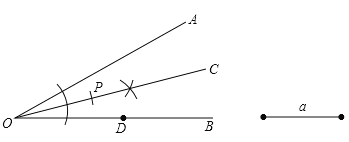
(2)如图,OP=a;
(3)∠OEP=∠ODP或∠OEP+∠ODP=180°.
理由是:以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,
PN⊥OB于N,则PM=PN.
在△E2PM和△DPN中,![]() ,
,
∴△E2PM≌△DPN(HL),
∴∠OE2P=∠ODP;
以P为圆心,以PD为半径作弧,交OA于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
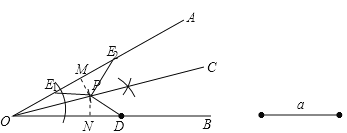
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图, ![]() 是等边三角形
是等边三角形![]() 内的一点,连结
内的一点,连结![]() 、
、![]() 、
、![]() ,以
,以![]() 为边作
为边作![]() 且
且![]() .连结
.连结![]() .
.
(1)观察并猜想![]() 与
与![]() 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.
(2)若![]() ,
, ![]() ,
, ![]() ,连结
,连结![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)在(2)的条件下,求![]() 的面积.
的面积.
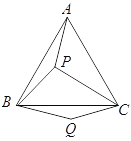
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 过一点有且只有一条直线与已知直线平行.
B. 在同一平面内,过一点有且只有一条直线与已知直线垂直.
C. 有公共顶点且有一条公共边的两个角互为邻补角.
D. 相等的两个角是对顶角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2009年初甲型HIN1流感在墨西哥爆发并在全球蔓延,研究表明,甲型HIN1流感球形病毒细胞的直径约为0.00000156 m,用科学记数法表示这个数是( )
A. 0.156×10-5m B. 0.156×105m C. 1.56×10-6m D. 1.56×106m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( )

A. 9.5 B. 10.5 C. 11 D. 15.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC边上的一点,以E为圆心,EC为半径的半圆与以A为圆心AB为半径的圆弧相外切于点F,若AB=4,
(1)求半圆E的半径r的长;
(2)求四边形ADCE的面积;
(3)连接DB、DF,设∠BDF=α,∠AEC=β,求证:β-2α=90°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com