
【题目】如图,在四边形ABCD中,AB∥CD,∠ECF=∠BCD=90°,CE=CF=5,BC=7,BD平分∠ABC,E是△BCD内一点,F是四边形ABCD外一点.(E可以在△BCD的边上)
(1)求证:DC=BC;
(2)当∠BEC=135°,设BE=a,DE=b,求a与b满足的关系式;
(3)当E落在线段BD上时,求DE的长.

【答案】(1)证明见解析;(2)b2-a2=50;(3)![]() 或
或![]() .
.
【解析】
(1)由角平分线定义得出∠ABD=∠CBD,由平行线的性质得出∠ABD=∠BDC,证出∠CBD=∠BDC,即可得出结论;
(2)证明△DCE≌△BCF(SAS),得出DE=BF,证出△CEF是等腰直角三角形,得出EF= ![]() CE=
CE=![]() ,∠CEF=45°,得出∠BEF=90°,在Rt△BEF中,由勾股定理即可得出结论;
,∠CEF=45°,得出∠BEF=90°,在Rt△BEF中,由勾股定理即可得出结论;
(3)由等腰直角三角形的性质得出BD=![]() BC=
BC=![]() ,∠CBD=∠CDB=45°,同(2)得△DCE≌△BCF(SAS),得出DE=BF,∠CBF=∠CDE=45°,证出∠EBF=90°,BE=BD-DE=
,∠CBD=∠CDB=45°,同(2)得△DCE≌△BCF(SAS),得出DE=BF,∠CBF=∠CDE=45°,证出∠EBF=90°,BE=BD-DE=![]() -DE,在Rt△BEF中,由勾股定理得出方程,解方程即可求出DE.
-DE,在Rt△BEF中,由勾股定理得出方程,解方程即可求出DE.
(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵AB∥CD,
∴∠ABD=∠BDC,
∴∠CBD=∠BDC,
∴DC=BC;
(2)解:由(1)得:DC=BC,
∵∠BCD=90°,∠ECF=90°,
∴∠DCE+∠BCE=∠BCF+∠BCE=90°,
∴∠DCE=∠BCF,
在△DCE和△BCF中,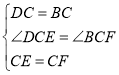 ,
,
∴△DCE≌△BCF(SAS),
∴DE=BF,
∵DE=b,
∴BF=b,
∵∠ECF=90°,CE=CF,
∴△CEF是等腰直角三角形,
∴EF=![]() CE=5
CE=5![]() ,∠CEF=45°,
,∠CEF=45°,
∵∠BEC=135°,
∴∠BEF=90°,
在Rt△BEF中,BE2+EF2=BF2,即a2+(5![]() )2=b2,
)2=b2,
∴b2-a2=50;
(3)解:如图,
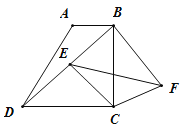
∵DC=BC,∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BD=![]() BC=7
BC=7![]() ,∠CBD=∠CDB=45°,
,∠CBD=∠CDB=45°,
同(2)得:△DCE≌△BCF(SAS),
∴DE=BF,∠CBF=∠CDE=45°,
∴∠EBF=∠CBD+∠CBF=45°+45°=90°,
∵BE=BD﹣DE=7![]() ﹣DE,
﹣DE,
∴在Rt△BEF中,EF2=BE2+BF2,即:(5![]() )2=(7
)2=(7![]() ﹣DE)2+DE2,
﹣DE)2+DE2,
解得:DE=4![]() 或DE=3
或DE=3![]() .
.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】关于二次函数![]() ,以下结论:①抛物线交
,以下结论:①抛物线交![]() 轴有两个不同的交点;②不论
轴有两个不同的交点;②不论![]() 取何值,抛物线总是经过一个定点;③设抛物线交
取何值,抛物线总是经过一个定点;③设抛物线交![]() 轴于
轴于![]() 、
、![]() 两点,若
两点,若![]() ,则
,则![]() ;④抛物线的顶点在
;④抛物线的顶点在![]() 图象上;⑤抛物线交
图象上;⑤抛物线交![]() 轴于
轴于![]() 点,若
点,若![]() 是等腰三角形,则
是等腰三角形,则![]() ,
,![]() ,
,![]() .其中正确的序号是( )
.其中正确的序号是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或解方程
(1)2![]() ﹣3
﹣3![]() +
+![]()
(2)(![]() ﹣2)(
﹣2)(![]() +2)﹣(
+2)﹣(![]() )2
)2
(3)(﹣3)0﹣![]() ﹣|1﹣
﹣|1﹣![]() |﹣
|﹣![]()
(4)3(3x﹣1)2﹣27=0
(5)![]() =﹣2
=﹣2
(6)![]() x﹣2=
x﹣2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=5,AB=1,点P是线段BC (不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,当BP= 时,△ADP是等腰直角三角形.(请直接写出答案)
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并加以证明.
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,请画出图形,并求线段B′D的长度.(参考定理:若直角△ABC中,∠C是直角,则BC2+AC2=AB2)
查看答案和解析>>
科目:初中数学 来源: 题型:
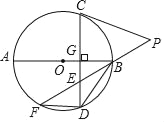
【题目】如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连结CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.
(1)求证:CD=BF;
(2)求证:PC是⊙O的切线;
(3)若tanF=![]() ,AG﹣BG=
,AG﹣BG=![]() ,求ED的值.
,求ED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com