
【题目】在体育中考项目中考生可在篮球、排球中选考一项.小明为了选择一项参加体育中考,将自己的10次测验成绩进行比较并制作了折线统计图,依据图中信息小明选择哪一项参加体育中考更合适,并说明理由,______.
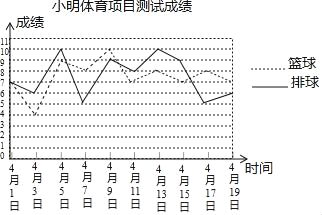
【答案】选择篮球参加中考,因为篮球和排球的平均得分相同,但篮球发挥更稳定.
【解析】
由折线统计图得出篮球和排球的成绩,分别计算其平均成绩和方差,据此分析可得.
由折线统计图知,篮球的成绩为:7、4、9、8、10、7、8、7、8、7,
排球的成绩为:7、6、10、5、9、8、10、9、5、6,
∵![]() =
=![]() ×(7+4+9+8+10+7+8+7+8+7)=7.5,
×(7+4+9+8+10+7+8+7+8+7)=7.5,
![]() =
=![]() ×(7+6+10+5+9+8+10+9+5+6)=7.5,
×(7+6+10+5+9+8+10+9+5+6)=7.5,
∴S篮球2=![]() ×[(7-7.5)2+(4-7.5)2+(9-7.5)2+(8-7.5)2+(10-7.5)2+(7-7.5)2+(8-7.5)2+(7-7.5)2+(8-7.5)2+(7-7.5)2]=2.25,
×[(7-7.5)2+(4-7.5)2+(9-7.5)2+(8-7.5)2+(10-7.5)2+(7-7.5)2+(8-7.5)2+(7-7.5)2+(8-7.5)2+(7-7.5)2]=2.25,
S排球2=![]() ×[(7-7.5)2+(6-7.5)2+(10-7.5)2+(5-7.5)2+(9-7.5)2+(8-7.5)2+(10-7.5)2+(9-7.5)2+(5-7.5)2+(6-7.5)2]=3.45,
×[(7-7.5)2+(6-7.5)2+(10-7.5)2+(5-7.5)2+(9-7.5)2+(8-7.5)2+(10-7.5)2+(9-7.5)2+(5-7.5)2+(6-7.5)2]=3.45,
由于![]() =
=![]() ,但S篮球2<S排球2,
,但S篮球2<S排球2,
则篮球和排球的平均得分相同,但篮球发挥更稳定,
所以选择篮球参加中考,
故答案为:篮球,理由:篮球和排球的平均得分相同,但篮球发挥更稳定.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
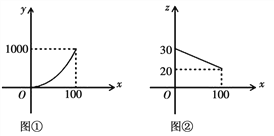
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用![]() 万元
万元![]() 与年产量
与年产量![]() 万件
万件![]() 之间的函数图象是顶点为原点的抛物线的一部分
之间的函数图象是顶点为原点的抛物线的一部分![]() 如图
如图![]() 所示
所示![]() ;该产品的销售单价
;该产品的销售单价![]() 元
元![]() 件
件![]() 与年销售量
与年销售量![]() 万件
万件![]() 之间的函数图象是如图
之间的函数图象是如图![]() 所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元
所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元![]() 毛利润
毛利润![]() 销售额
销售额![]() 生产费用
生产费用![]()
![]() 请写出y与x以及z与x之间的函数关系式;
请写出y与x以及z与x之间的函数关系式;
![]() 求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进节能减排,发展低碳经济,某市“用电大户”用480万元购得“变频调速技术”后,进一步投入资金1520万元购买配套设备,以提高用电效率达到节约用电的目的.已知该“用电大户”生产的产品“草甘磷”每件成本费为40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利为w(万元).(年获利=年销售额-生产成本-节电投资)
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该“用电大户”是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
(3)若该“用电大户”把“草甘磷”的销售单价定在超过100元,但不超过200元的范围内,并希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利为1842万元,请你确定此时销售单价.在此情况下,要使产品销售量最大,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+2与x轴交于点A,与y轴交于点B,与反比例函数![]() (x<0)的图象交于点C,点D(3,a)在直线y=﹣x+2上,连接OD,OC,若∠COD=135°,则k的值为( )
(x<0)的图象交于点C,点D(3,a)在直线y=﹣x+2上,连接OD,OC,若∠COD=135°,则k的值为( )
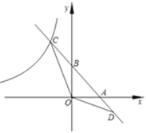
A. ﹣2 B. ﹣4 C. ﹣6 D. ﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
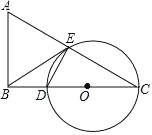
【题目】如图,在△ABC 中,∠ABC=90°,∠C=30°,AC 的垂直平分线交 BC 于点 D,交AC 于点 E.
(1)判断 BE 与△DCE 的外接圆⊙O 的位置关系,并说明理由;
(2)若 BE=![]() ,BD=1,求△DCE 的外接圆⊙O 的直径.
,BD=1,求△DCE 的外接圆⊙O 的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
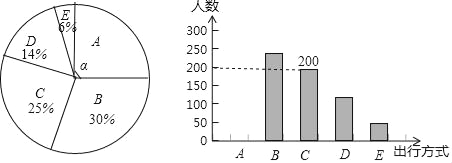
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图. 根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD为⊙O的直径,BC为⊙O的切线,切点为M,分别过A,D两点作BC的垂线,垂足分别为B,C,AD的延长线与BC相交于点E.
(1)求证:△ABM∽△MCD;
(2)若AD=8,AB=5,求ME的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com