Question

【题目】如图，在平面直角坐标系中，抛物线y=﹣x2+bx+c的图象交x轴于A（4，0），B（﹣1，0）两点，交y轴于点C，连结AC．

(1)填空：该抛物线的函数解析式为 ，其对称轴为直线 ；

(2)若P是抛物线在第一象限内图象上的一动点，过点P作x轴的垂线，交AC于点Q，试求线段PQ的最大值；

(3)在（2）的条件下，当线段PQ最大时，在x轴上有一点E（不与点O，A重合），且EQ=EA，在x轴上是否存在点D，使得△ACD与△AEQ相似？如果存在，请直接写出点D的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）证明见解析.

【解析】

（1）把代入抛物线中列方程组，解出可得b和c的值，可得抛物线的解析式，配方成顶点式可得对称轴；
（2）先利用待定系数法求直线AC的解析式，再设点P的坐标，并表示点Q的坐标，根据铅直高度表示PQ的长，并配方可得PQ的最大值；
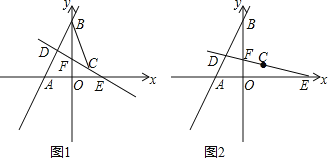
（3）分两种情况：①当D在线段OA上时，如图1，根据△AEQ∽△ADC，由EQ=EA，得CD=AD，利用勾股定理解决问题；②当D在点B的左侧时，如图2根据三角形相似，由EQ=EA可得OA=OD，可得D的坐标．

．解：（1）把代入抛物线中得：

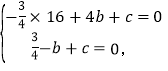
解得：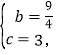

∴

∴抛物线的函数解析式为：其对称轴为直线：

故答案为：

(2)∵A(4,0),C(0,3)，

∴直线AC的解析式为：

设,则

∴

∵P是抛物线在第一象限内图象上的一动点，

∴0<x<4，

∴当x=2时，PQ的最大值为3；

(3)分两种情况：

①当D在线段OA上时,如图1,△AEQ∽△ADC，

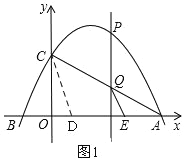
∵EQ=EA,

∴CD=AD，

设CD=a，则AD=a，OD=4a，

在Rt△OCD中,由勾股定理得：

∴

∴

∴

②当D在点B的左侧时,如图2,△AEQ∽△ACD，

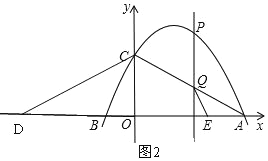
∵EQ=EA，

∴CD=AC，

∵OC⊥AD，

∴OD=OA=4，

∴D(4,0)，

综上所述,当△ACD与△AEQ相似时,点D的坐标为或(4,0).