
分析 (1)由二次项系数非零结合根的判别式△>0,即可得出关于k的一元一次不等式组,解之即可得出k的取值范围;
(2)由根与系数的关系可得出x1+x2=-$\frac{k+2}{k}$、x1•x2=$\frac{1}{4}$,将其代入k2x12-4kx1•x2+k2x22=k2(x1+x2)2-2k2x1•x2-4kx1•x2=12中可得出关于k的一元二次方程,解之可得出k的值,再由(1)的结论可确定k值.
解答 解:(1)∵关于x的方程kx2+(k+2)x+$\frac{k}{4}$=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}{k≠0}\\{△=(k+2)^{2}-4×k×\frac{k}{4}>0}\end{array}\right.$,
解得:k>-1且k≠0.
∴k的取值范围为k>-1且k≠0.
(2)∵原方程的两根分别为x1、x2,
∴x1+x2=-$\frac{k+2}{k}$,x1•x2=$\frac{1}{4}$.
∵k2x12-4kx1•x2+k2x22=k2(x1+x2)2-2k2x1•x2-4kx1•x2=12,
∴(k+2)2-$\frac{1}{2}$k2-k=12,
解得:k1=-8,k2=2.
∵k>-1且k≠0,
∴k的值为2.
点评 本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)根据二次项系数非零结合根的判别式△>0,列出关于k的一元一次不等式组;(2)根据根与系数的关系结合k2x12-4kx1x2+k2x22=12,列出关于k的一元二次方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
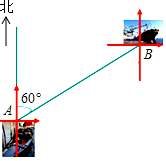 天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.9h来估计,其中h(单位:m)是眼睛离海平面的高度.
天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.9h来估计,其中h(单位:m)是眼睛离海平面的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
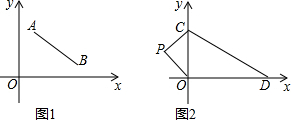 已知,在平面直角坐标系中,A(1,a),B(b,1),其中a,b满足$\sqrt{2a-b-2}$+(a+b-7)2=0.
已知,在平面直角坐标系中,A(1,a),B(b,1),其中a,b满足$\sqrt{2a-b-2}$+(a+b-7)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:
某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:| 卖出价格x(元/件) | 50 | 51 | 52 | 53 |
| 销售量p(件) | 500 | 490 | 480 | 470 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
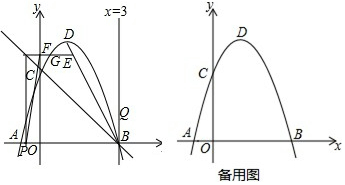
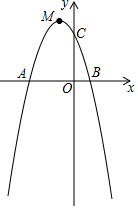 如图,抛物线与x轴交于点A(-3,0),B(1,0)两点,与y轴交于点C(0,3).
如图,抛物线与x轴交于点A(-3,0),B(1,0)两点,与y轴交于点C(0,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com