
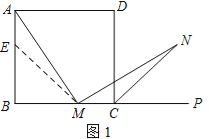
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
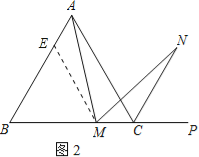
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)


图1 图2
【答案】(1)证明见解析(2)仍然成立 (3) ![]()
【解析】试题分析:(1)要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.
(2)同(1),要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.
(3)由(1)(2)可知,∠AMN等于它所在的正多边形的一个内角即等于![]() 时,结论AM=MN仍然成立.
时,结论AM=MN仍然成立.
(1)证明:在边AB上截取AE=MC,连接ME.
∵正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,
BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=45°,∴∠AEM=135°.
∵N是∠DCP的平分线上一点,
∴∠NCP=45°,∴∠MCN=135°.
在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,
∴△AEM≌△MCN(ASA),
∴AM=MN.
(2)解:结论AM=MN还成立
证明:在边AB上截取AE=MC,连接ME.
在正△ABC中,∠B=∠BCA=60°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAE,
BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=60°,∴∠AEM=120°.
∵N是∠ACP的平分线上一点,
∴∠ACN=60°,∴∠MCN=120°.
在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,
∴△AEM≌△MCN(ASA),
∴AM=MN.
(3)解:若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,则当∠AMN=![]() 时,结论AM=MN仍然成立.
时,结论AM=MN仍然成立.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.

(1)求AD的长;
(2)当△PDC的面积为15平方厘米时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 问题与探索
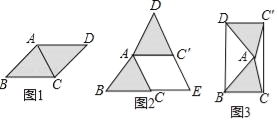
问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 .
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
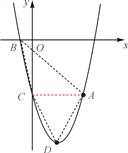
【题目】如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)连接AB、BC、CD、DA,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.
(1)求证:PC=PG;
(2)当点G是BC的中点时,求证:![]() ;
;
(3)已知⊙O的半径为5,在满足(2)的条件时,点O到BC的距离为![]() ,求此时△CGP的面积.
,求此时△CGP的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com