
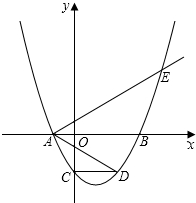
 如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),
如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),分析 (1)利用抛物线与y轴的交点坐标即可得出结论;
(2)令y=0,确定出A,B的坐标,利用AB=4,即可求出a,m的值,即可得出结论;
(3)先判断出△ADM∽△AEN,得出$\frac{AM}{AN}$=$\frac{AD}{AE}=\frac{DM}{EN}$,再求出A,B,C的坐标,进而求出点E的坐标,即可求出ENM即可得出结论.
解答 解:(1)∵抛物线y=a(x2-2mx-3m2)=ax2-2amx-3am2,
∵-3am2=-3,
∴a=$\frac{1}{m^2}$,
(2)令y=0,∴0=a(x2-2mx-3m2)=a(x-3m)(x+m),
∴x=3m或x=-m,
∵m>0,
∴A(-m,0),B(3m,0),
∵AB=4,
∴3m-(-m)=4,∴m=1,
由(1)知,a=$\frac{1}{{m}^{2}}$,
∴a=1,
∴抛物线解析式为y=x2-2x-3,
(3)定值为$\frac{3}{5}$.
如图,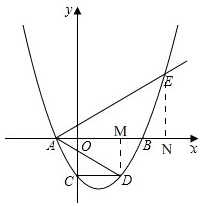 过D、E作x轴的垂线段,垂足为M、N.
过D、E作x轴的垂线段,垂足为M、N.
∴∠AMD=∠ANE=90°,
∵AB平分∠DAE,
∴∠DAB=∠EAB,
∴△ADM~△AEN,∴$\frac{AM}{AN}$=$\frac{AD}{AE}=\frac{DM}{EN}$,
由(2)知,A(-m,0),B(3m.0),C(0,-3),
∵CD∥AB,令y=0=-3,
∴a(x2-2mx-3m2)=-3①,
∵a=$\frac{1}{{m}^{2}}$②,
联立①②得,x=0(舍)或x=2m,
∴D(2m,-3),
∴AM=2m-(-m)=3m,DM=3,
设E(x,$\frac{1}{{m}^{2}}$(x2-2mx-3m2),
∴AN=x+m,EN=$\frac{1}{{m}^{2}}$(x2-2mx-3m2),
∴$\frac{3m}{x+m}=\frac{3}{\frac{1}{{m}^{2}}({x}^{2}-2mx-3{m}^{2})}$,
∴x=-m(舍)或x=4m,
∴EN=$\frac{1}{{m}^{2}}$(16m2-2m×4m-3m2)=5,
∴$\frac{AD}{AE}=\frac{DM}{EN}$=$\frac{3}{5}$.
点评 此题是二次函数综合题,主要考查了抛物线与x轴的交点坐标,相似三角形的性质,解本题的关键是求出EN,是一道基础题目.


科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:单选题
下列方程①3x2-x=0;②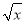 +x2=1;③3x+
+x2=1;③3x+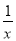 =0:④2x2-l=(x -l)( x -2);⑤(5x -2)(3x -7)=15x2,其中是一元二次方程的有( )
=0:④2x2-l=(x -l)( x -2);⑤(5x -2)(3x -7)=15x2,其中是一元二次方程的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
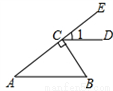
A. 35° B. 45° C. 55° D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
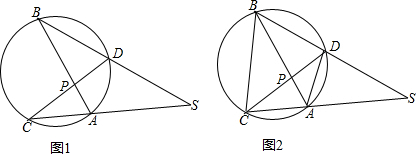
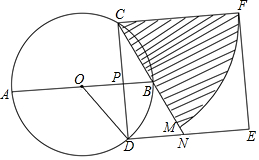 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
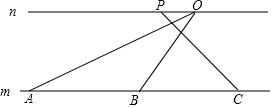
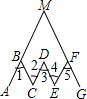 完成推理填空
完成推理填空查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com