
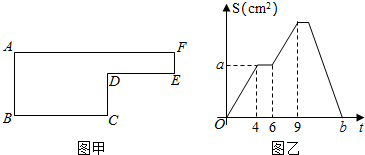
分析 (1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度可得BC的长;又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
(2)分析图形可得,甲中的图形面积等于AB×AF-CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案.
解答 解:(1)动点P在BC上运动时,对应的时间为0到4秒,易得:BC=2cm/秒×4秒=8cm;
a=$\frac{1}{2}$×BC×AB=24cm2.
根据题意,动点P共运动了BC+CD+DE+EF+FA=8+4+6+2+14=34cm,
其速度是2cm/秒,则b=$\frac{34}{2}$=17秒;
故答案为:8cm;24;17;
(2)由图可得:CD=2×2=4cm,DE=2×3=6cm,
则AF=BC+DE=14cm,
又由AB=6cm,
则甲图的面积为AB×AF-CD×DE=60cm2,
答:图甲中的图形面积的60cm2.
点评 本题考查动点问题的函数图象,解题的关键是读懂图意,明确横轴与纵轴的意义.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
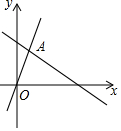 如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A (m,3),则不等式2x<ax+4的解集为( )| A. | $x<\frac{3}{2}$ | B. | $x>\frac{3}{2}$ | C. | x<3 | D. | x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3(x2-4y2) | B. | 3(x+2y)(x-2y) | C. | 3(2x+y)(2x-y) | D. | 3(x-2y)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2+0.5x | B. | y=2+x | C. | y=2+2x | D. | y=2x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{4}$x2+$\frac{9}{4}$与直线y=-$\frac{1}{2}$x+$\frac{3}{2}$交于点A,C的两点,点B是点A关于y轴的对称点.
如图,抛物线y=-$\frac{1}{4}$x2+$\frac{9}{4}$与直线y=-$\frac{1}{2}$x+$\frac{3}{2}$交于点A,C的两点,点B是点A关于y轴的对称点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com