
如图是用硬纸板做成的四个全等的直角三角形
(两直角边长分别是a、b,斜边长为c)和一个边长为c的正方形,请你将它们拼成一个能验证勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)写出验证勾股定理的过程.
|
分析:利用拼图验证勾股定理,关键是要抓住直角三角形的斜边长与正方形的边长相等.拼图的方式一般有两种:一是在正方形的外面放三角形,二是在正方形的里面放三角形.验证勾股定理的思路就是抓住图形的面积相等. 解: (1)如图所示.(只要画出一个图形即可)
(2)如图①.因为大正方形的面积表示为(a+b)2,也可表示为c2+ 所以 (a+b)2=c2+所以 a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方. 如图②.因为大正方形的面积表示为 c2,也可表示为所以 c2=所以 c2=a2+b2.即直角三角形两直角边的平方和等于斜边的平方. 点评:本例的解题过程与课本中的探索方法是一样的,都是构造一个图形,利用两种方法计算该图形的面积,从而得到一个关于直角三角形三边长 a、b、c之间的两个等式,这种方法在数学学习中有着广泛的运用. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
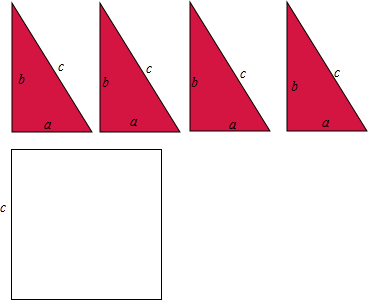 直角边长分别是a,b,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
直角边长分别是a,b,斜边长为c和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
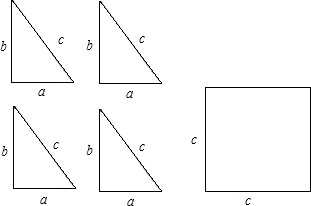 如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是a、b,斜边长为c)和一个正方形(边长为c).请你将它们拼成一个能验证勾股定理的图形.
如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是a、b,斜边长为c)和一个正方形(边长为c).请你将它们拼成一个能验证勾股定理的图形.查看答案和解析>>
科目:初中数学 来源:2012届安徽省安庆市八年级第二学期质量检测数学卷 题型:解答题
如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是a,b,斜边长为c)和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形,并利用此图形证明勾股定理.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com