
【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H. 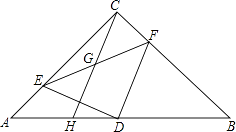
(1)若E在边AC上. ①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
【答案】
(1)解:①连接CD,
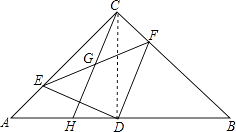
∵∠ACB=90°,D为AB的中点,AC=BC,
∴CD=AD=BD,
又∵AC=BC,
∴CD⊥AB,
∴∠EDA+∠EDC=90°,∠DCF=∠DAE=45°,
∵DF⊥DE,
∴∠EDF=∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中
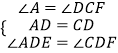
∴△ADE≌△CDF,
∴DE=DF.
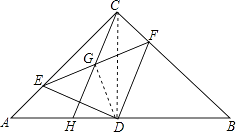
②连接DG,
∵∠ACB=90°,G为EF的中点,
∴CG=EG=FG,
∵∠EDF=90°,G为EF的中点,
∴DG=EG=FG,
∴CG=DG,
∴∠GCD=∠CDG
又∵CD⊥AB,
∴∠CDH=90°,
∴∠GHD+∠GCD=90°,∠HDG+∠GDC=90°,
∴∠GHD=∠HDG,
∴GH=GD,
∴CG=GH.
(2)解:如图,当E在线段AC上时,

∵CG=GH=EG=GF,
∴CH=EF=5,
∵△ADE≌△CDF,
∴AE=CF=3,
∴在Rt△ECF中,由勾股定理得: ![]() ,
,
∴AC=AE+EC=3+4=7;
如图,当E在线段CA延长线时,
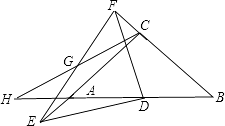
AC=EC﹣AE=4﹣3=1,
综合上述AC=7或1.
【解析】(1)①连接CD,推出CD=AD,∠CDF=∠ADE,∠A=∠DCB,证△ADE≌△CDF即可;②连接DG,根据直角三角形斜边上中线求出CG=EG=GF=DG,推出∠GCD=∠GDC,推出∠GDH=∠GHD,推出DG=GH即可;(2)求出EF=5,根据勾股定理求出EC,即可得出答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,
(1) 取点M(1,0),则点M到直线l: ![]() 的距离为_________,取直线
的距离为_________,取直线![]() 与直线l平行,则两直线距离为_________.
与直线l平行,则两直线距离为_________.
(2) 已知点P为抛物线y=x2-4x的x轴上方一点,且点P到直线l: ![]() 的距离为
的距离为![]() ,求点P的坐标.
,求点P的坐标.
(3) 若直线y=kx+m与抛物线y=x2-4x相交于x轴上方两点A、B(A在B的左边),且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离的最大时直线y=kx+m的解析式.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;则其中说法正确的是( ).

A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)在信宜市某“三华李”种植基地有A,B两个品种的树苗出售,已知A种比B种每株多2元,买1株A种树苗和2株B种树苗共需20元.
(1)问A,B两种树苗每株分别是多少元?
(2)为扩大种植,某农户准备购买A,B两种树苗共360株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据图填空:
(1)如图①,△ABE,△ACD都是等边三角形,若CE=6,则BD的长=; 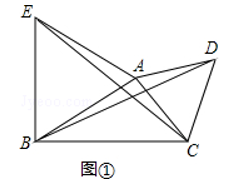
(2)如图②,△ABC中,∠ABC=30°,AB=3,BC=4,D是△ABC外一点,且△ACD是等边三角形,则BD的长= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是圆锥(如图1)底面的直径,P是圆锥的顶点,此圆锥的侧面展开图如图2所示.一只蚂蚁从A点出发,沿着圆锥侧面经过PB上一点,最后回到A点.若此蚂蚁所走的路线最短,那么M,N,S,T(M,N,S,T均在PB上)四个点中,它最有可能经过的点是( ) 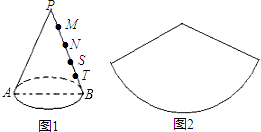
A.M
B.N
C.S
D.T
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com