
分析 根据平均数的计算公式先求出这组数据的平均数,再根据方差公式进行计算即可.
解答 解:平均数=$\frac{1}{5}$(2+1+0+3+4)=2,
则方差S2=$\frac{1}{5}$[(2-2)2+(1-2)2+(0-2)2+(3-2)2+(4-2)2]=2.
故答案为:2.
点评 本题考查了方差:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


科目:初中数学 来源: 题型:解答题
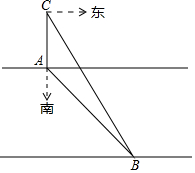 某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)
某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
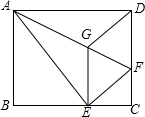 如图,将矩形ABCD沿线段AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿线段AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com