
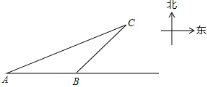
【题目】一艘轮船自西向东航行,在![]() 处测得东偏北
处测得东偏北![]() 方向有一座小岛
方向有一座小岛![]() ,继续向东航行
,继续向东航行![]() 海里到达
海里到达![]() 处,测得小岛
处,测得小岛![]() 此时在轮船的东偏北
此时在轮船的东偏北![]() 方向上.之后,轮船继续向东航行多少海里,距离小岛
方向上.之后,轮船继续向东航行多少海里,距离小岛![]() 最近?
最近?
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):甲公司: 4,5,5,5,5,7,9,12,13,15;
乙公司: 6,6,8,8,8,9,10,12,14,15;
丙公司: 4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)甲、乙、丙三家公司在该产品的销售中都声称,其销售的该产品的使用寿命是8年,你如何理解他们的宣传.(请用已学的统计量中加以说明)
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
(3)如果你是丙公司的推销员,你将如何结合上述数据,对本公司的产品进行推销?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+3)x+3m=0.
(1)求证:无论m取什么实数值,该方程总有两个实数根.
(2)若该方程的两实根x1和x2是一个矩形两邻边的长且该矩形的对角线长为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
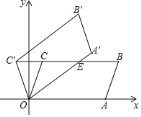
【题目】如图,在平面直角坐标系![]() 中,平行四边形
中,平行四边形![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将平行四边形
,将平行四边形![]() 绕点
绕点![]() 逆时针方向旋转得到平行四边形
逆时针方向旋转得到平行四边形![]() ,当点
,当点![]() 落在
落在![]() 的延长线上时,线段
的延长线上时,线段![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长度为________.
的长度为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
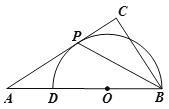
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AC相切于点P.
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com