
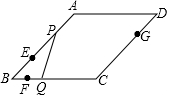
 如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )
如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )| A. | 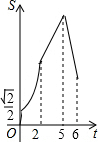 | B. | 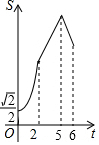 | C. | 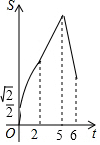 | D. | 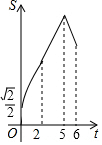 |
分析 分三种情形求出S与t的关系即可解决问题.
解答 解:当0<t≤2时,点P在AB上,点Q在BC上,
S=$\frac{1}{2}$•(1+t)•(2+2t)•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$(t+1)2,
当2<t≤5时,点P在AD上,点Q在BC上,
S=$\frac{1}{2}$•(1+t)•3$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$(t+1),
当5<t≤6时,点P、点Q在CD上,
S=$\frac{1}{2}$•[6-(t-5)-(2t-10)]•3$\sqrt{2}$=-$\frac{9\sqrt{2}}{2}$t+$\frac{63\sqrt{2}}{2}$.
故选A.
点评 本题考查动点问题函数应用、菱形的性质、三角形的面积、分段函数等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,属于中考常考题型.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
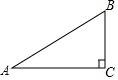 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
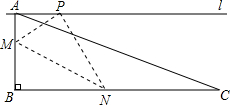 如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )| A. |  | B. | 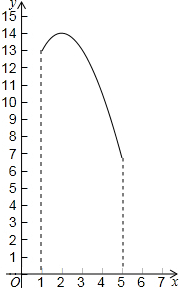 | ||
| C. | 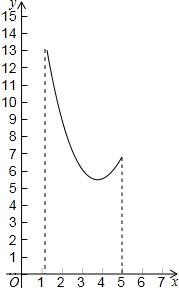 | D. | 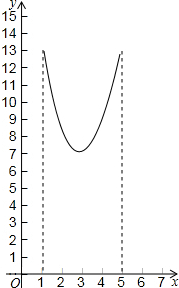 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
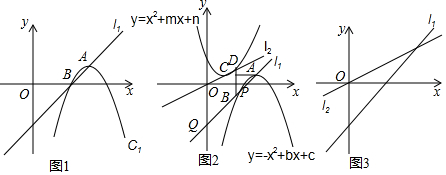
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
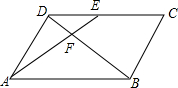 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=1:2,FB=12,则DF=( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com